Понятие функции. Предел функции

Правило f, сопоставляющее каждому значению xÎD (область определения) единственное значение yÎG (область значений), называется числовой функцией, заданной на множестве D и принимающей значения в области G. (Предполагается, что D, G 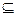R)

Обозначение: y=f(x).

Способы задания функций

1) Табличный

Таблица значений живой массы бычка в зависимости от возраста.

2) Аналитический

Живая масса (y) телят до одного года (в кг) может быть выражена функцией:

y=378,4-419,6 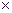e^-0,0001x,

где x – потребление полностью усвояемого питательного вещества (в кг)

3) Графический

График формирования зрелого почвенного профиля: 0 – ноль–момент, начало почвообразования,

p=p(t) – толщина почвенного слоя, как функция времени,

t_m – время образования зрелого почвенного профиля.

Предел функции

Пусть aÎR и функция f(X) определена в некоторой окрестности точки a: XÎ(a-e,a+e) (e>0). Можно представить себе ряд последовательностей X_n, сходящихся к точке a, значения которой лежит в области определения f(X) (X_nÎD(f))

Число A называется пределом функции f(X) в точке X=a, если для любой числовой последовательности X_n, сходящейся к а (X_nÎD(f), X_n¹a "n), последовательность соответствующих значений функции y_n=f(X_n) сходится и ее предел равен А.

Пишут: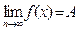

Пример: Доказать, что функция 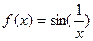не имеет предела при х=0.

4Рассмотрим две последовательност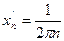и и 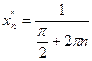(n=1,2,..)

Ясно, что 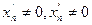и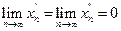

Значения соответствующих последовательностей:

,

,

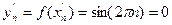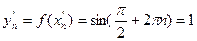
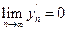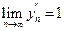
Нашлись две последовательности 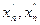, сходящиеся к 0, такие что, соответствующие значения пределов функции в них разные. Пришли к противоречию с определением предела. Функция f(x) не имеет предела при X=0.