Понятия: последовательность, предел последовательности.
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Предел и непрерывность функций
Понятия: последовательность, предел последовательности.
Упорядоченное множество вещественных чисел, любое из которых имеет свой номер, называется последовательностью.
Обозначение: {Xn}=X0, X1, X2, …Xn, …
Задача 1: Популяция микроорганизмов первоначально имела массу 100 мг и постоянно увеличивалась с темпом роста 20% в час.
Какова масса популяции через 10 часов роста? Через какое время масса популяции возрастет десятикратно?
4Пусть Xn соответствует массе популяции через n часов роста. По условию X0 =10 мг, Xn+1=1,2  Xn. Значит X1=(1,2)
Xn. Значит X1=(1,2)  X0; X2=(1,2)2
X0; X2=(1,2)2  X0; Xn=(1,2)n
X0; Xn=(1,2)n 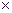 X0 =10
X0 =10 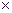 (1,2)n
(1,2)n
Через 10 часов X10=10 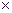 (1,2)10»61,92 мг.
(1,2)10»61,92 мг.
Через 13 часов X13=10 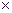 (1,2)13»107 мг, т. е. происходит увеличение биомассы более чем в 10 раз.
(1,2)13»107 мг, т. е. происходит увеличение биомассы более чем в 10 раз.
Число a называют пределом последовательности Xn, если для любого 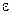 >0 найдется такой номер N, начиная с которого выполнятся:
>0 найдется такой номер N, начиная с которого выполнятся:
 |
|Xn-a|<
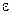 при n³N
при n³N
Записывается: 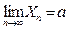
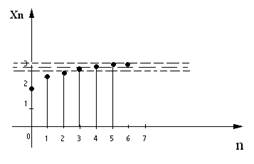
Задача 2: Численность Xn популяции изменяется в соответствии с законом 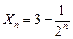 (n=0, 1, ..)
(n=0, 1, ..)
Найти 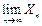 и в соответствии с определением предела найти номер N, если
и в соответствии с определением предела найти номер N, если 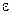 =0,1
=0,1
6 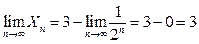
Если 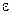 =0,1 Þ
=0,1 Þ 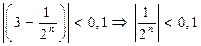
n=1 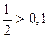
n=2 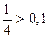
n=3 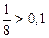
n=4 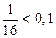
Итак, если N=4, то для всех n³N
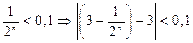
Последовательность Xn – монотонная, если она либо возрастает 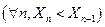 , либо убывает
, либо убывает 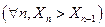 .
.
Последовательность X n – ограничена, если найдутся числа m, MÎR: m£ X n £M ("nÎN).
Последовательность 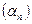 называют бесконечно малой, если
называют бесконечно малой, если 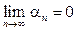 . Последовательность
. Последовательность 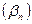 - бесконечно большая, если
- бесконечно большая, если 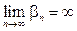 . Коротко: an – б. м,
. Коротко: an – б. м,
bn – б. б.
Выполняется соотношение: 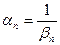 ,
, 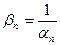 .
.
Пример 1 Вычислить пределы:
1) 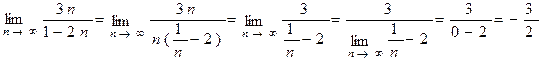
2) 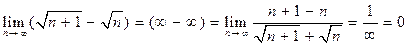 .
.
Дата добавления: 2016-06-05; просмотров: 1788;











