Свойства пределов последовательностей

1. Если последовательность a_n – ограничена и монотонна, то она сходится (т. е. имеет предел)

2. Если последовательности a_n, b_n – сходятся, то:

a)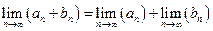

b)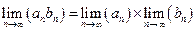

c) 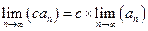(c= const)

d) 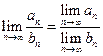(при условии )

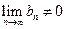e)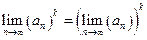

3. Если 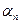- б. м., g_n – ограничена, то 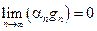, т. е. a_ng_n – б. м.

Пример 2 Найти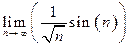

4Имеем произведение двух последовательностей:

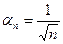– б. м. и b_n=sin (n) – ограничена (–1£ sin (n) £ 1)

В соответствии со свойством (3): 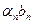- б. м. и .

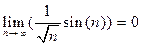Задача 3 (Ряд Фибоначчи)

Сформулирована знаменитым итальянским математиком Леонардо из Пизы (прозванным Фибоначчи) в книге об абаке в 1202 году. Суть в подсчете потомства от одной пары кроликов (включая родительскую пару) по месяцам, если известно, что через месяц пара кроликов производит на свет другую пару, а рожают кролики регулярно со второго месяца после рождения. Такая своего рода математическая модель воспроизводства кроликов может быть проиллюстрирована графическим деревом (дендрограммой) размножения и описывается числовым рядом (рядом Фибоначчи):

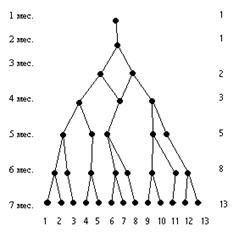
Если обозначим u_n – общее количество образовавшихся пар кроликов в n ^й месяц, то для последовательности

u_n = 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,...

Закономерно выполняется u_n+2=u_n+u_n+1.

Вопрос: сколько пар кроликов образуется от одной пары через год?

4Достаточно вычислить 12 членов ряда Фибоначчи:

u_n=1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233

т. е. через год от одной пары кроликов (если принять за начало отсчета новорожденную пару) образуется 233 пары кроликов (включая родительскую).