Изображение синусоидально изменяющихся величин Э.Д.С., напряжений и токов векторами на комплексной плоскости. Векторные топографические диаграммы (В.Т.Д.).
В современной технике широкое распространение получили электрические цепи, в которых ЭДС, напряжения, токи изменяются во времени по синусоидальному закону.
Для анализа электрического состояния цепей с синусоидально изменяющимися токами и напряжениями применяются различные формы представления синусоидальных функций в виде:
- тригонометрических функций;
- комплексных чисел.
Для их графической иллюстрации используют:
- графики мгновенных значений;
- векторные диаграммы.
Переменные гармонические (синусоидальные) напряжения и токи являются синусоидальными функциями времени:
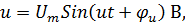
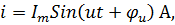
| где u, i, и 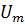 , , 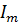 - мгновенные и амплитудные значения напряжения и тока соответственно; - мгновенные и амплитудные значения напряжения и тока соответственно;
| |
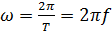 - угловая частота, рад/с; f - частота, Гц; T-период, с; - угловая частота, рад/с; f - частота, Гц; T-период, с;
| ||
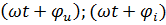 - фаза, рад/с; - фаза, рад/с;
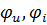 - начальные фазы напряжения и тока; - начальные фазы напряжения и тока;
| 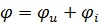 -период, с; -период, с;
| |
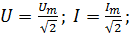 - действующие значения напряжения и тока. - действующие значения напряжения и тока.
| ||
Гармонические (синусоидальные) напряжения и ток представлены через комплексные числа;
| Для амплитудных значений | Для действующих значений |
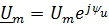 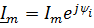
| 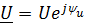 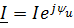
|
Графические иллюстрации этих синусоидальных величин есть:
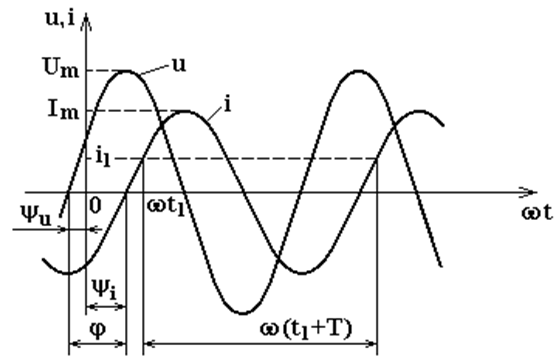
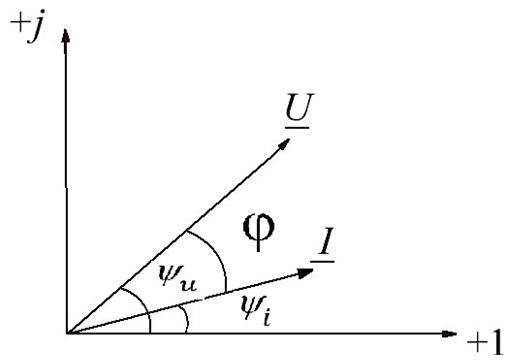
| 
|
| График мгновенных значений (зависимость мгновенных значений напряжения тока в функции времени) | Векторная диаграмма (представление комплексов напряжения, тока на комплексной плоскости) |
Задача 2.1
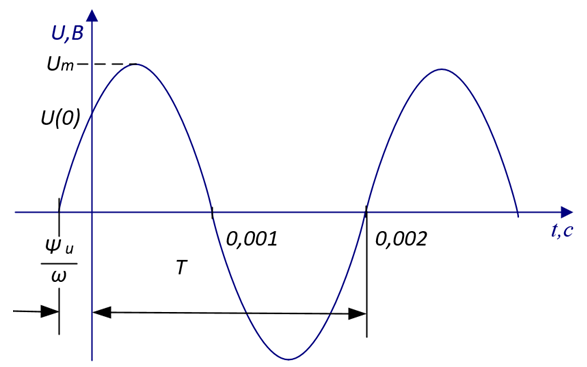
| Синусоидальное напряжение задано в виде графика мгновенных значений: Um=20 В; Т=0,002 с; U(0)=10 В. | ||
| Представить напряжение в виде: 1) тригонометрической функции времени; 2) комплексного числа; 3) вектора на комплексной плоскости | |||
| Решение задачи 2.1 | |||
| 1. Для представления синусоидаль-ного напряжения в виде тригоно-метрической функции времени | - угловую частоту 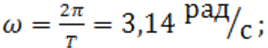 - начальную фазу
- начальную фазу 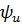 . .
| ||
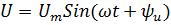 необходимо определить:
необходимо определить:
| Тогда: 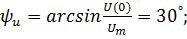
| ||
2. Комплексная амплитуда напряжения:
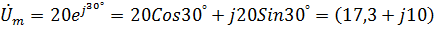 B. B.
| |||
Комплекс действующего значения напряжения:
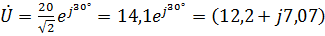 B.
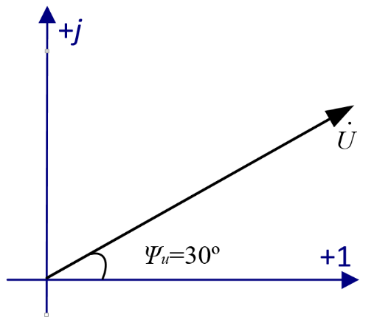
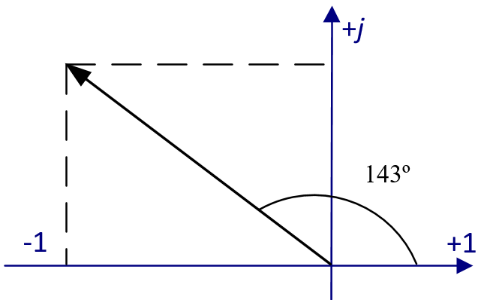
3. Комплекс действующего значения напряжения на комплексной плоскости: B.
3. Комплекс действующего значения напряжения на комплексной плоскости:
| 
| ||
Задача 2.2
Синусоидальный ток, заданный графиком мгновенных значений, представить в виде: 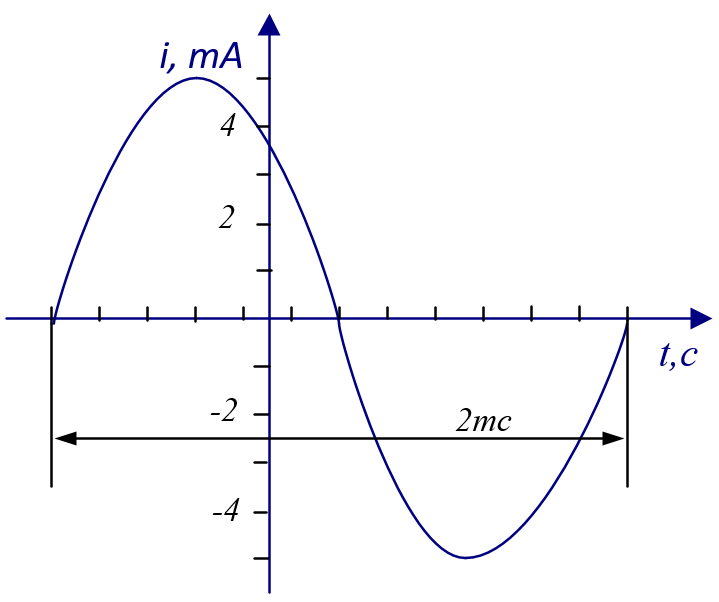
| ||
| 1) тригонометрической функции времени; 2) комплексного числа; 3) изобразить в виде вектора на комплексной плоскости. | ||
| Решение задачи 2.2. | ||
1. Так как 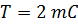 , то , то 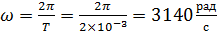
| ||
Начальная фаза 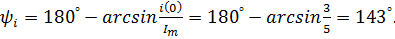
| ||
| Тогда ток в тригонометрической форме: | 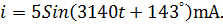
| |
| ||
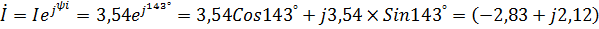
| ||
Определение: Совокупность векторов на комплексной плоскости построенных с соблюдением правильной ориентации их относительно друг друга и отображающих процессы, происходящие в цепях называется векторной диаграммой.
Дата добавления: 2021-12-14; просмотров: 664;











