Комплексные числа и действия над ними.
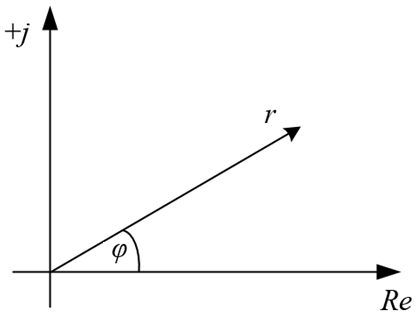
| 1. 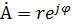 - показательная форма. - показательная форма.
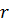 - модуль комплексного числа; - модуль комплексного числа; 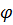 -аргумент
2. Используя формулу Эйлера -аргумент
2. Используя формулу Эйлера
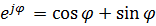 Получим тригонометрическую форму
Получим тригонометрическую форму
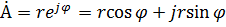
| |||||||
| 3. Обозначить через | a 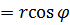 - действительную часть
b = - действительную часть
b = 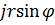 - мнимую часть - мнимую часть
| |||||||
| Получим алгебраическую форму комплексного числа | 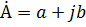
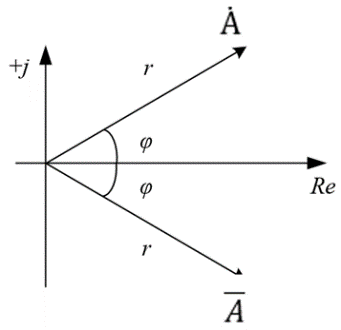
| 
| ||||||
Связь 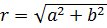 и и 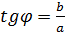
| ||||||||
| Комплексно-сопряженным комплексному числу: | ||||||||
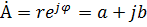
| является: | 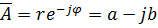 . .
| ||||||
| Произведение | 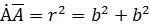
| - всегда положительное число; | ||||||
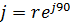
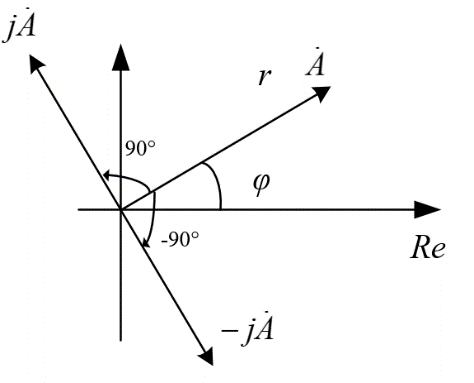
| - оператор поворота вектора в положительном направ-лении на 90 градусов | |||||||
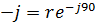
| - оператор поворота вектора в отрицательном направлении на 90 градусов | |||||||
Запись мнимых частей комплексно-сопряженных чисел принимает вид:
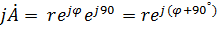
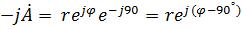
| 
|
Действия над комплексными числами
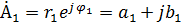 , , 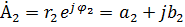 . .
| (2.3) |
1. Сложение и вычитание выражений в алгебраической форме
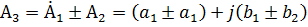 . .
| (2.4) |
2. Умножение выражений (2.3) в показательной и в алгебраической формах
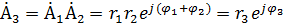 ; ;
| (2.5) |
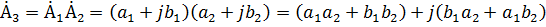 . .
| (2.6) |
3. Деление выражений (2.3) в показательной и в алгебраической формах
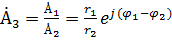 ; ;
| (2.7) |
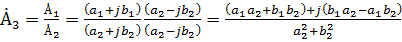 . .
| (2.8) |
Полная мощность в комплексной форме
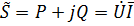 , ,
| (2.9) |
где P - активная мощность; 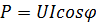 ; Q - реактивная мощность,
; Q - реактивная мощность, 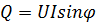 ;
; 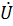 - комплекс действующего значения напряжения на участке цепи,
- комплекс действующего значения напряжения на участке цепи, 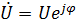 ;
; 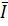 - сопряженный комплекс действующего значения тока на участке цепи,
- сопряженный комплекс действующего значения тока на участке цепи, 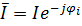 .
.
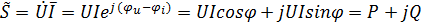 , ,
| (2.9) |
где 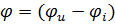 - разность фаз
- разность фаз
Баланс мощностей
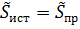 ; ;
| 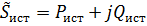 ; ;
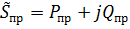 ; ;
| 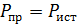 : :
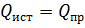 . .
|
3.5. Основы символического метода 
Задача 2.3. Написать комплекс действующего значения синусоидальной функции времени: 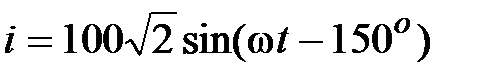 , А.
, А.
Решение: Модуль комплекса действующего значения совпадает с действующим значением синусоидальной величины, а аргумент совпадает с начальной фазой этой величины: 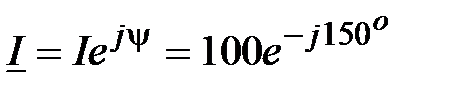 , А.
, А.
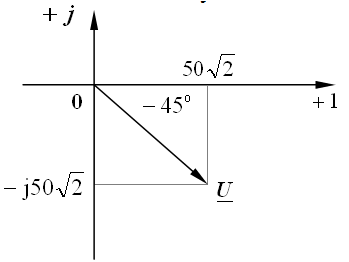
Задача 2.4. Написать комплекс действующего значения синусоидальной функции времени: 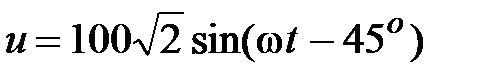 , В.
, В.
Решение:
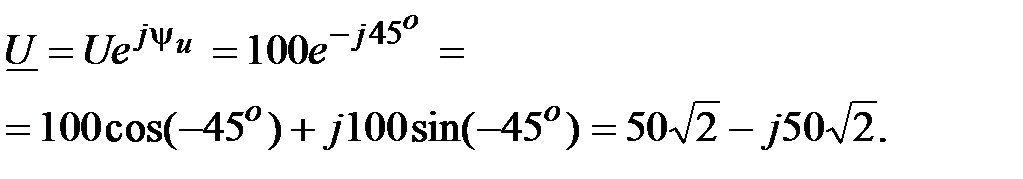
| 
|
Задача 2.5. Написать комплекс действующего значения синусоидальной функции времени: 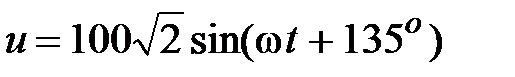 , B.
, B.
Решение:
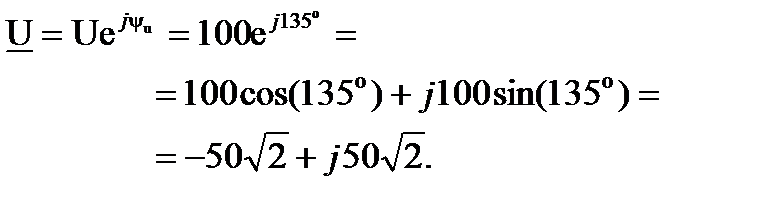
| 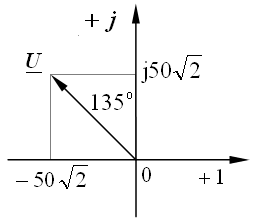
|
Задача 2.6. Написать комплекс действующего значения синусоидальной функции времени: 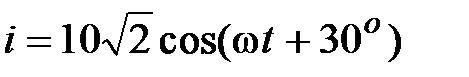 , А.
, А.
Решение: 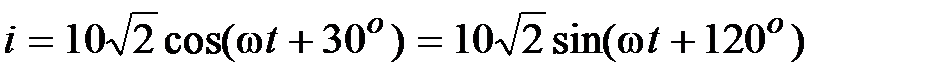 , А.
, А.
Отсюда 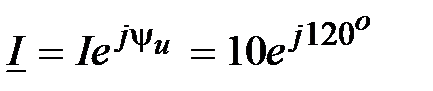 , А.
, А.
Задача 2.7. Написать комплекс действующего значения синусоидальной функции времени: 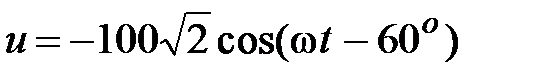 , В.
, В.
Решение:
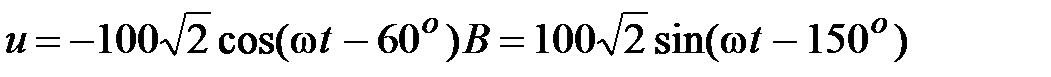 , B. , B. 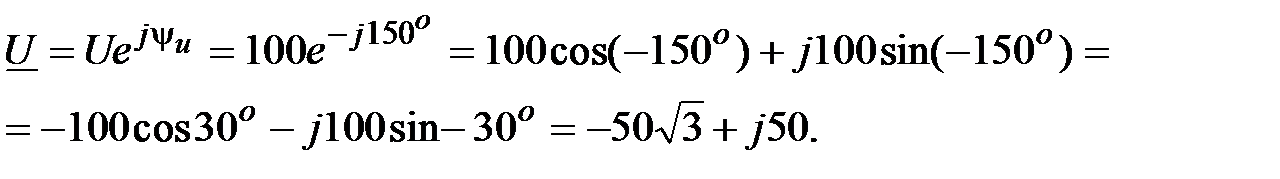
| 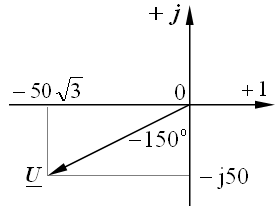
|
Задача 2.8. Найти синусоидальную функции времени, изображенную комплексом действующего значения: 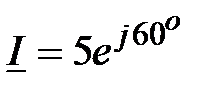 , A.
, A.
Решение: 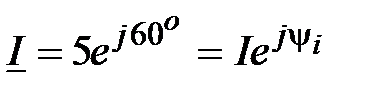 , oтсюда
, oтсюда 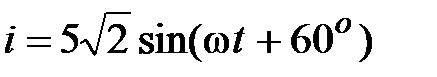 , A.
, A.
Задача 2.9. Найти синусоидальную функции времени, изображенную комплексом действующего значения: 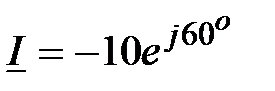 , A.
, A.
Решение:
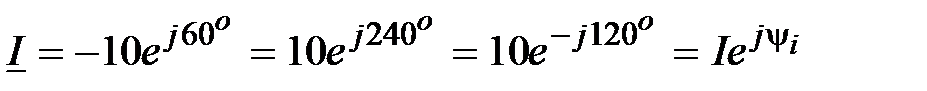 ,
(т.к. ,
(т.к. 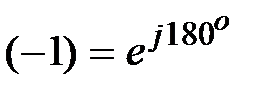 ).
Отсюда ).
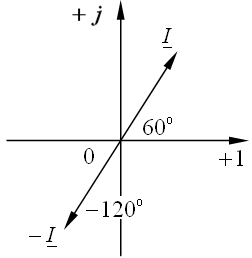
Отсюда 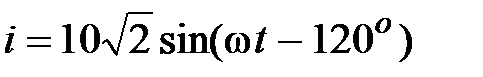 , A. , A.
| 
|
Задача 2.10. Найти синусоидальную функции времени, изображенную комплексом действующего значения: 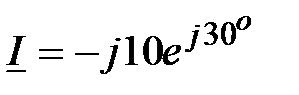 , A.
, A.
Решение:
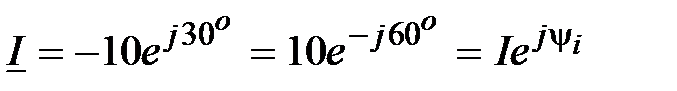 ,
(т.к. ,
(т.к. 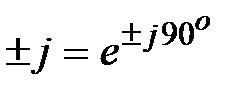 ).
Отсюда ).
Отсюда 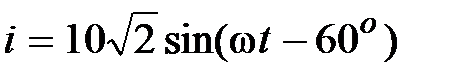 , A. , A.
| 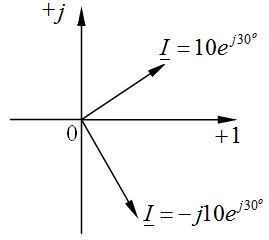
|
Задача 2.11. Найти синусоидальную функции времени, изображенную комплексом действующего значения: 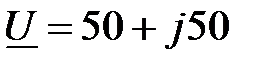 , В.
, В.
Решение:
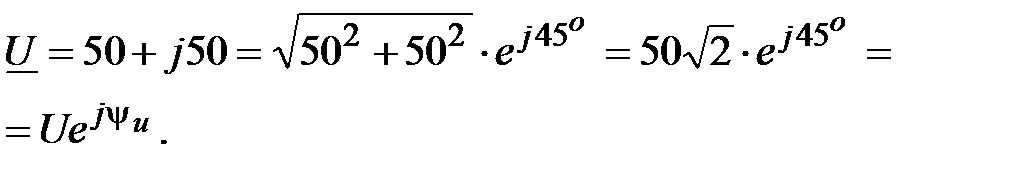 Отсюда
Отсюда 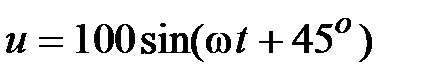 , В. , В.
| 
|
Задача 2.12. Найти синусоидальную функции времени, изображенную комплексом действующего значения: 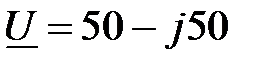 , В.
, В.
Решение:
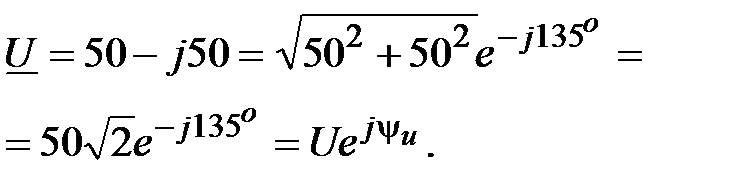 Отсюда
Отсюда 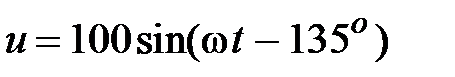 , В. , В.
| 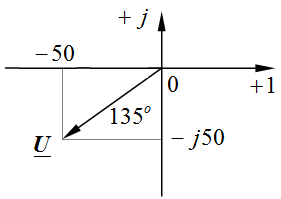
|
Задача 2.13. Найти синусоидальную функции времени, показанную комплексом действующего значения: 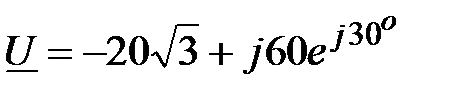 , В.
, В.
Решение:
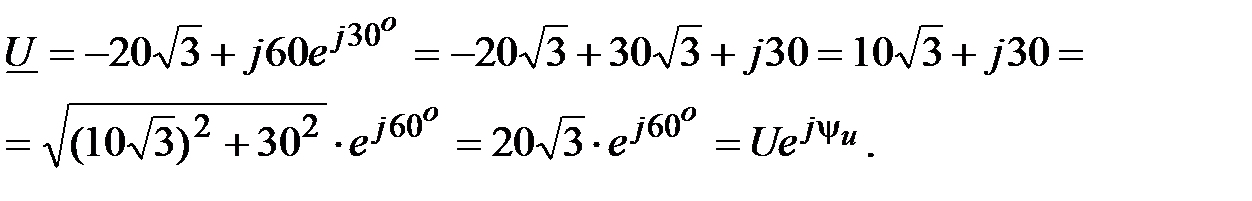 Отсюда
Отсюда 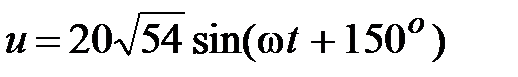 , В. , В.
| 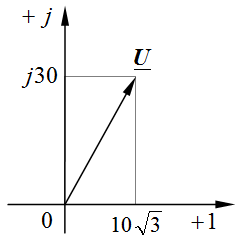
|
Задача 2.14. Найти синусоидальную функции времени, показанную комплексом действующего значения: 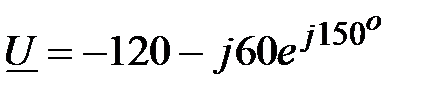 , В.
, В.
Решение:
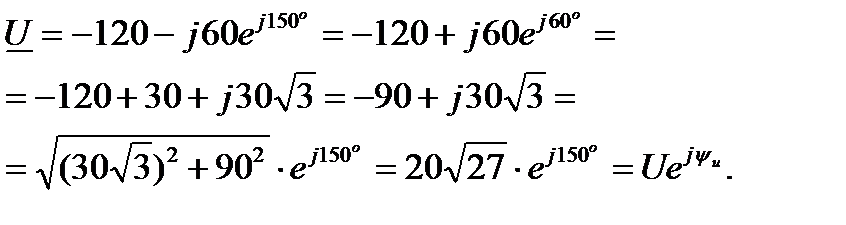 Отсюда
Отсюда 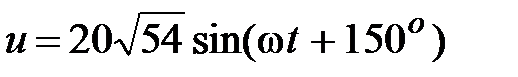 , В. , В.
| 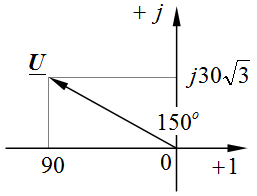
|
Задача 2.15. Определить сдвиг фаз 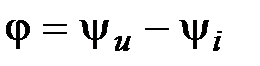 между напряжением и током, комплексы действующих значений которых равны:
между напряжением и током, комплексы действующих значений которых равны: 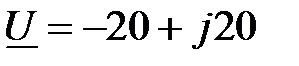 , B,
, B, 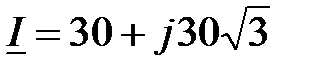 , A.
, A.
Решение:
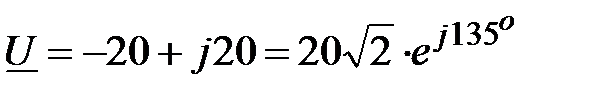 , B , , B , 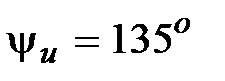 ; ;
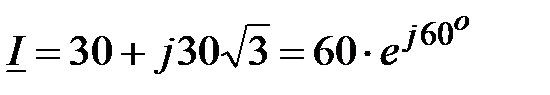 , A , , A , 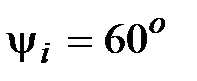 ; ;
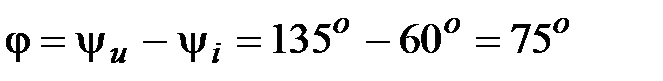 .
Отсюда .
Отсюда 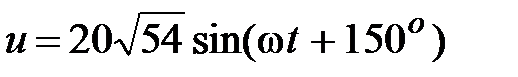 , В. , В.
| 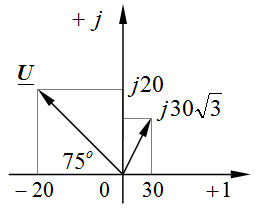
|
Задача 2.16. Определить комплексное сопротивление, т.к. напряжение и ток равны: 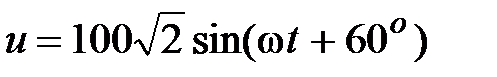 ,В;
,В; 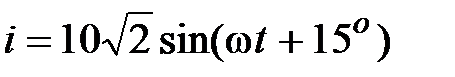 , А.
, А.
Решение: На основании закона Ома 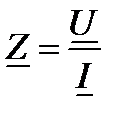
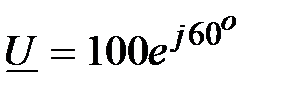 В,
В, 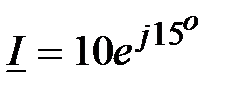 , А;
, А; 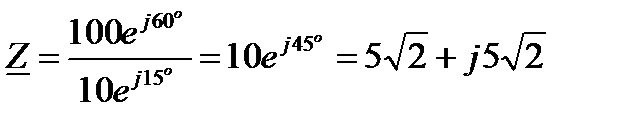 .
.
Задача 2.17. Определить мгновенное значение падения напряжения, если известны ток 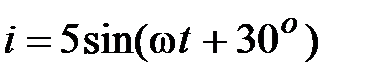 , А, и комплексное сопротивление
, А, и комплексное сопротивление 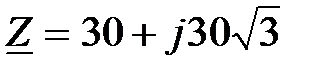 , Ом.
, Ом.
Решение: На основании закона Ома 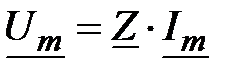 ;
;
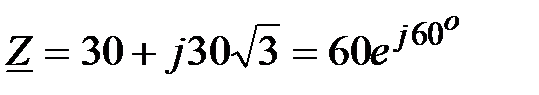 , Ом,
, Ом, 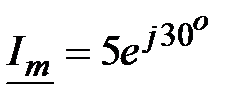 , А;
, А;
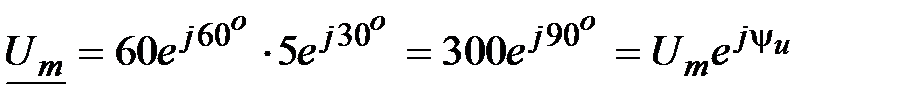 , В.
, В.
Отсюда 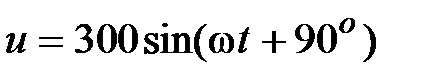 , В.
, В.
Задача 2.18. Определить мгновенное значение напряжения при токе 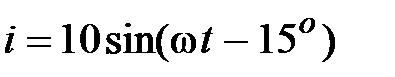 ,А, и комплексной проводимости
,А, и комплексной проводимости 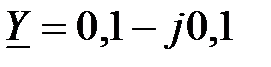 .
.
Решение: На основании закона Ома 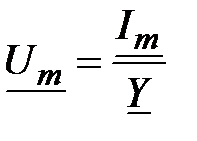 ;
;
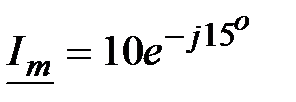 А,
А, 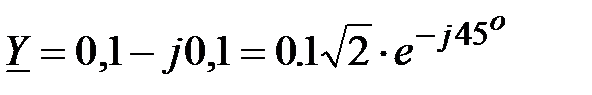 ;
;
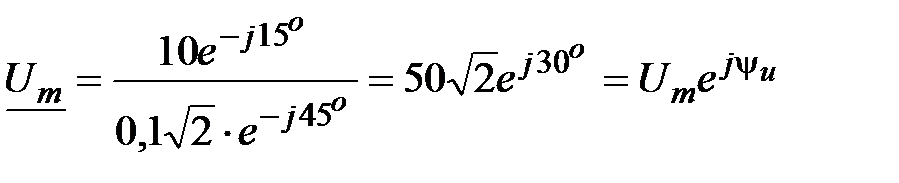 .
.
Отсюда 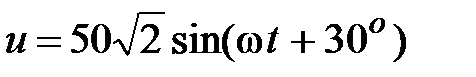 , В.
, В.
Задача 2.19. Найти сумму токов 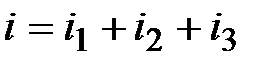 , мгновенные значения которых равны:
, мгновенные значения которых равны: 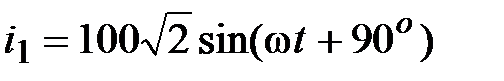 , А,
, А, 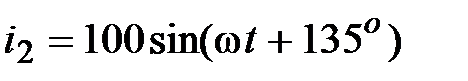 , А,
, А, 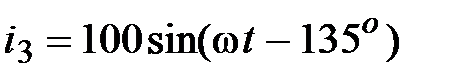 , А.
, А.
Решение: 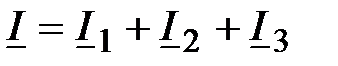 ; ;
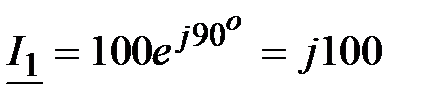 , А. , А. 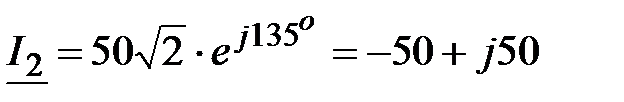 , А. , А.
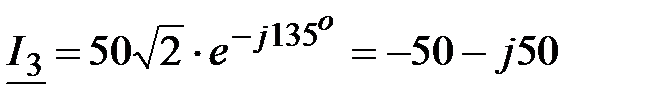 , А. , А.
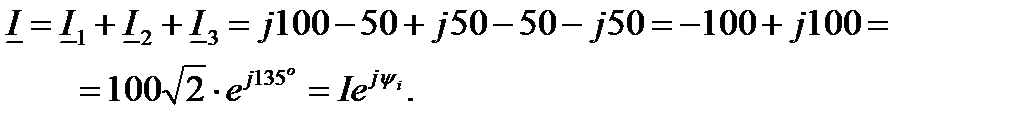 Отсюда
Отсюда 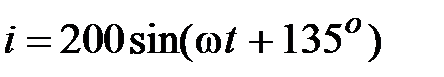 , А. , А.
| 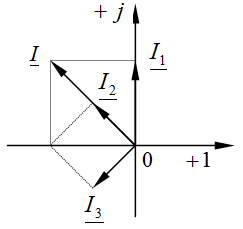
|
Задача 2.20. Определить 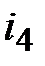 , если известно:
, если известно:
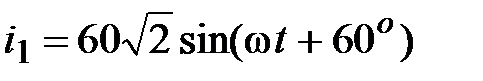 , А, , А, 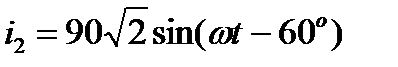 , А, , А,
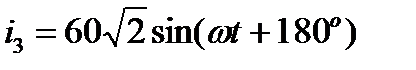 , А. , А.
| 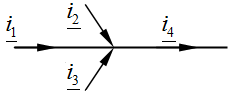
| |
Решение: На основании первого закона Кирхгофа: 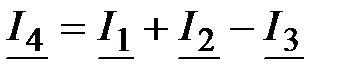 ; ;
| ||
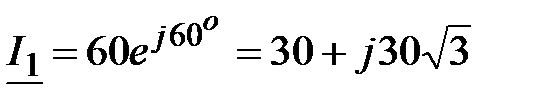 , A; , A;
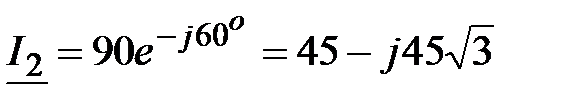 , A, , A, 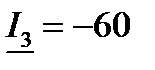 A; A;
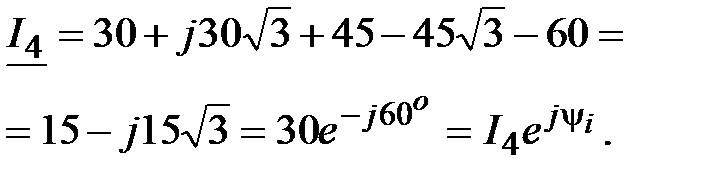 Отсюда
Отсюда 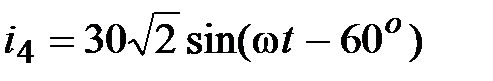 , А. , А.
| 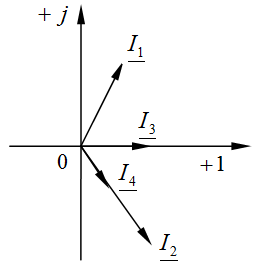
| |
Задача 2.21. Определить проводимость Y , если известно комплексное сопротивление 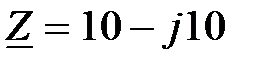 Ом.
Ом.
Решение: 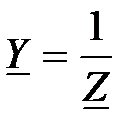 ;
; 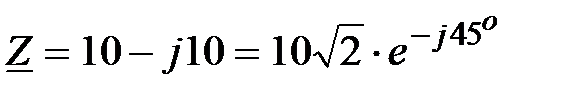 , Ом, тогда
, Ом, тогда
Отсюда 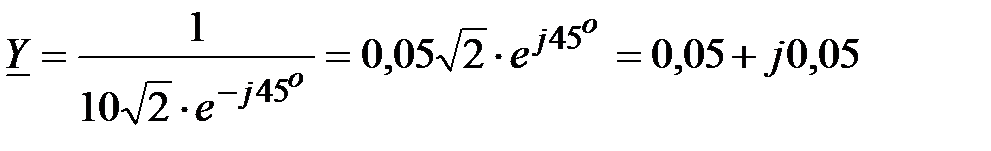 .
.
Задача 2.22. Найти выражение для комплексного сопротивления Z и комплексной проводимости Y, если 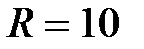 Oм,
Oм, 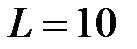 Гн,
Гн, 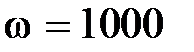 с-1 .
с-1 .
Решение: 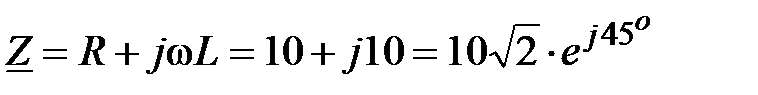 , Ом. , Ом.
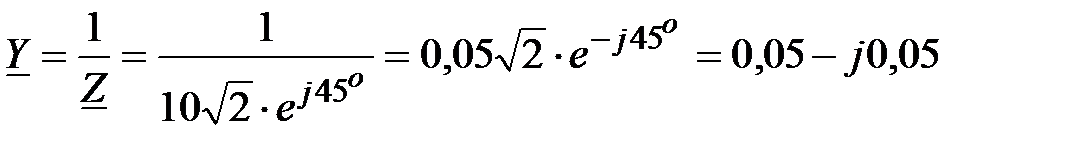 . .
| 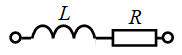
|
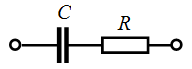
Задача 2.23. Найти выражение для комплексного сопротивления Z и комплексной проводимости Y , если 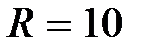 Oм,
Oм, 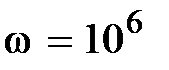 c-1,
c-1, 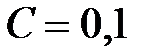 мкФ.
мкФ.
Решение:
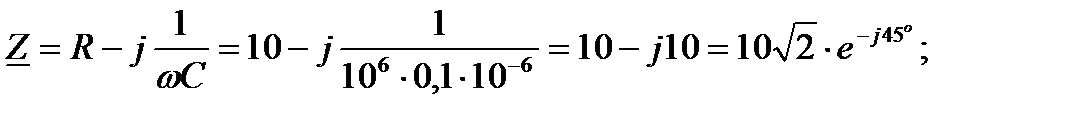
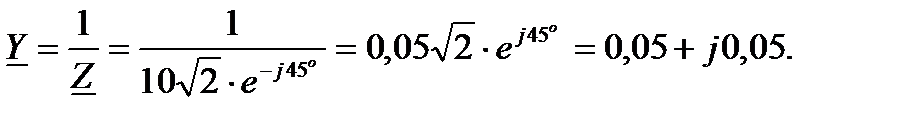
| 
|
Задача 2.25. Определить комплекс полной мощности, если 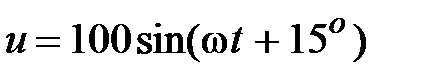 , В,
, В, 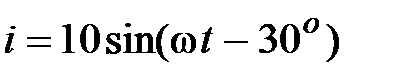 , А.
, А.
Решение: 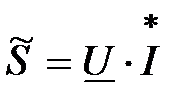 ;
;
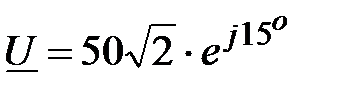 , В,
, В, 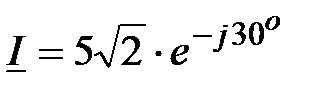 , А,
, А, 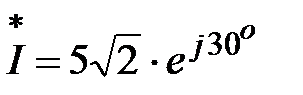 , А;
, А;
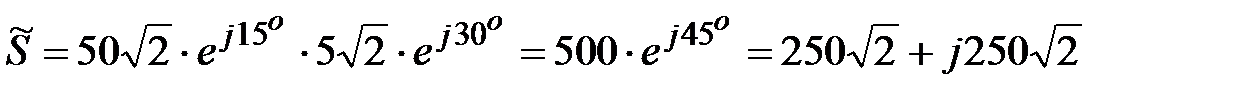 .
.
Задача 2.26. Определить активную и реактивную мощности, если 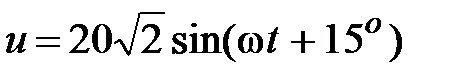 , В,
, В, 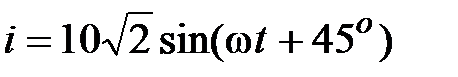 , А.
, А.
Решение: 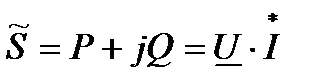 ;
;
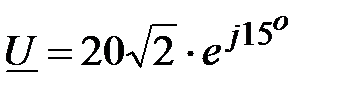 , В,
, В, 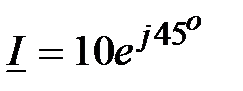 , А,
, А, 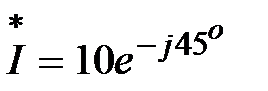 , А;
, А;
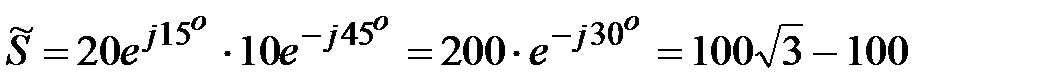 .
.
Отсюда 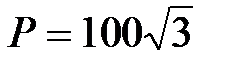 , Вт,
, Вт, 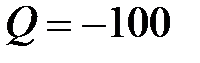 , вар.
, вар.
Задача 2.27. Известны ток и напряжение : 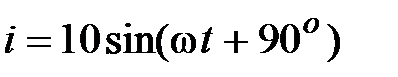 , А,
, А, 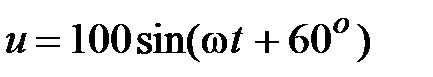 , В. Определить активную и реактивную мощности.
, В. Определить активную и реактивную мощности.
Решение: 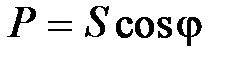 ,
, 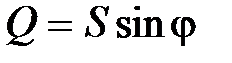 ,
,
где 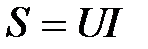 ;
; 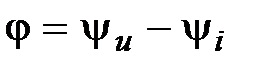 .
.
Отсюда
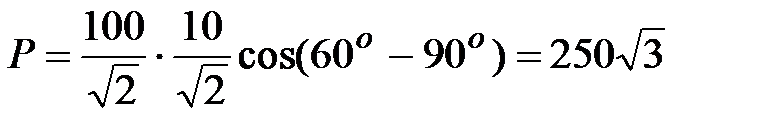 , Вт;
, Вт;
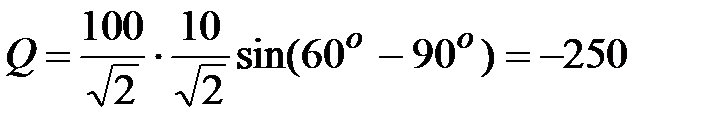 , вар.
, вар.
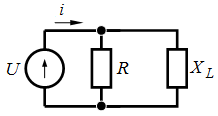
Задача 2.28. Определить сопротивление схемы (R и L), если 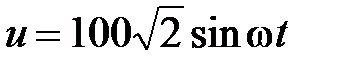 , В,
, В, 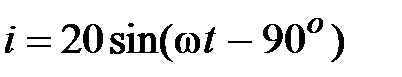 , А.
, А.
Решение:
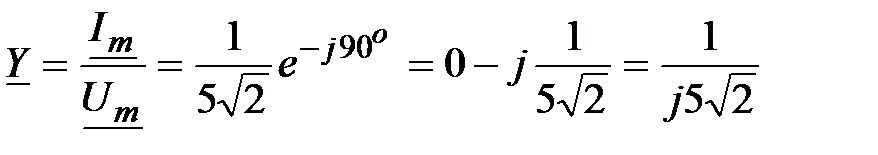 .
Отсюда .
Отсюда 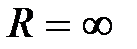 , , 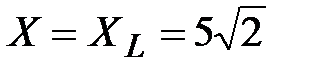 , Ом. , Ом.
| 
|
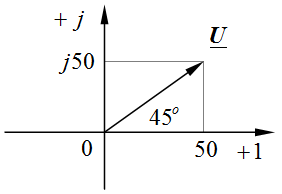
Задача 2.29. Синусоидально изменяющееся во времени напряжение задано в виде комплекса действующего значения
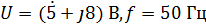
1. Построить на комплексной плоскости.
2. Представить тригонометрической функцией времени.
3. Начертить график мгновенных значений.
Решение: 1. Заданный комплекс представлен в алгебраической форме записи. Построим его на комплексной плоскости, отложив на осях действительных и мгновенных чисел соответствующие величины:
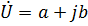 , , 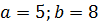 . .
| |
2. Для перехода от комплексного к тригонометрической форме записи напряжения представим комплекс в показательной форме:
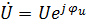 .
.
Модуль комплекса 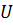 – действующее значение напряжения
– действующее значение напряжения
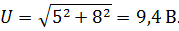
Амплитуда 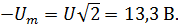
Аргумент комплексного числа – начальная фаза синусоидальной функции 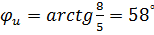 .Тогда
.Тогда 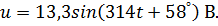
Амплитуда 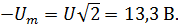 Аргумент комплексного числа – начальная фаза синусоидальной функции
Аргумент комплексного числа – начальная фаза синусоидальной функции 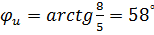 .
Тогда .
Тогда 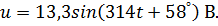
| 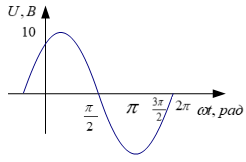 3. График мгновенных значений
3. График мгновенных значений
|
Задача 2.30.
Дано: 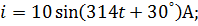
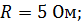
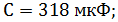
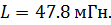
Определить комплексные напряжения 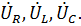
Записать мгновенные значения 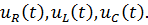
Изобразить векторную диаграмму напряжений и тока.
Решение: 1. Согласно алгоритму, заменяем мгновенные значения напряжений и тока расчетной схемы на их комплексные изображения.
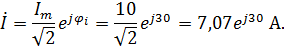 2. Индуктивное сопротивление равно:
2. Индуктивное сопротивление равно:
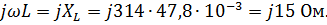
| | ||
3. Ёмкостное сопротивление равно:
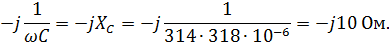 5. По закону Ома для участка цепи:
5. По закону Ома для участка цепи:
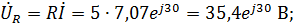
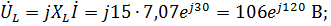
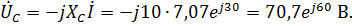 6. Мгновенные значения:
6. Мгновенные значения:
| | ||
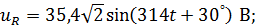
| 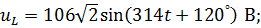
| 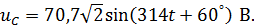
| |
Дата добавления: 2021-12-14; просмотров: 622;











