РАСЧЁТ ЦЕПЕЙ СИМВОЛИЧЕСКИМ МЕТОДОМ
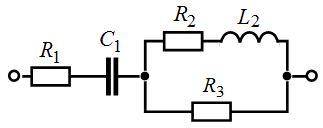
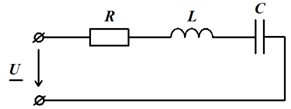
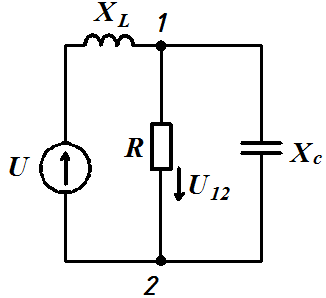
Задача 3.1. Определить комплексное сопротивление Z, если 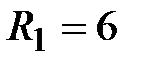 Oм,
Oм, 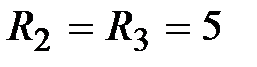 Oм,
Oм, 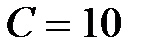 мкФ,
мкФ, 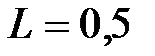 мГн,
мГн, 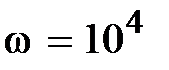 c-1.
c-1.
Решение: 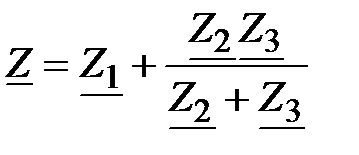 ,
где ,
где 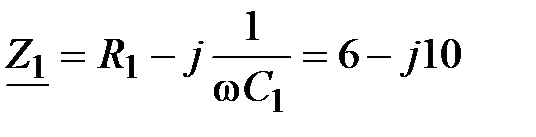 , Ом; , Ом;
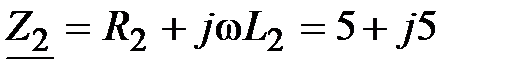 , Ом, , Ом,
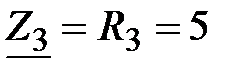 , Ом; , Ом;
| 
|
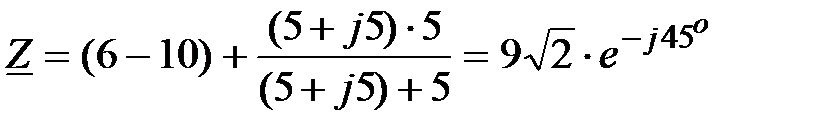 . .
|
Задача 3.2. Определить мгновенное значение тока 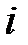 , если
, если 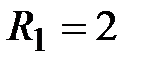 Oм,
Oм, 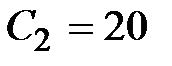 мкФ,
мкФ, 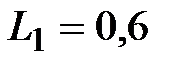 мГн,
мГн, 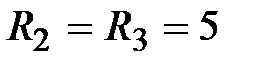 Oм,
Oм, 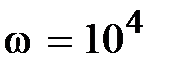 c-1,
c-1, 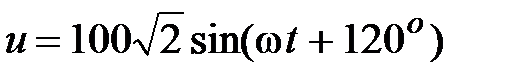 , В.
, В.
Решение: На основе закона Ома: 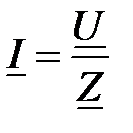 , , 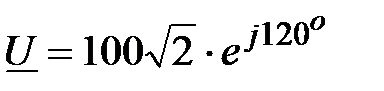 , , 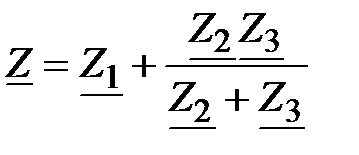 ; ;
| |
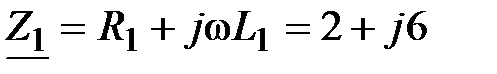 , Ом; , Ом;
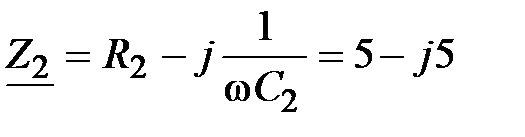 , Ом; , Ом;
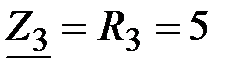 , Ом;
Отсюда , Ом;
Отсюда 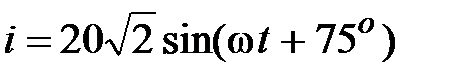 , А. , А.
| 
|
Задача 3.3. Определить мгновенные значения напряжения uL и uC, если 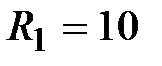 Oм,
Oм,  мкФ,
мкФ, 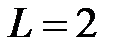 мГн,
мГн, 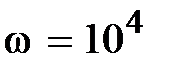 c-1,
c-1, 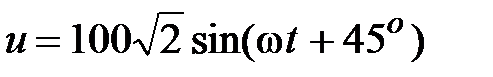 , В;
, В;
| Решение: На основе закона Ома: | 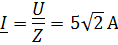
| |
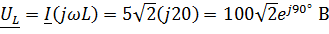
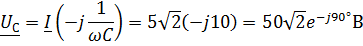 Откуда
Откуда 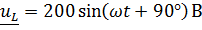 , ,
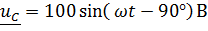
| 
| |
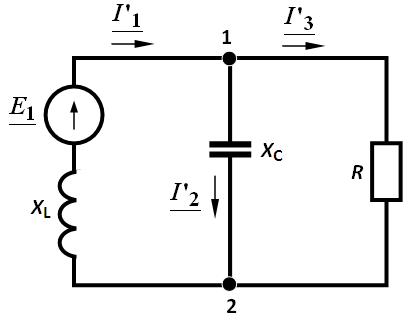
Задача 3.4.
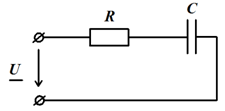
Дана цепь 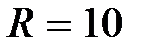 Ом, Ом, 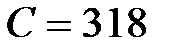 мкФ, мкФ, 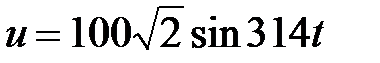 , В. Определить , В. Определить 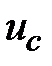 . .
| 
|
Решение: 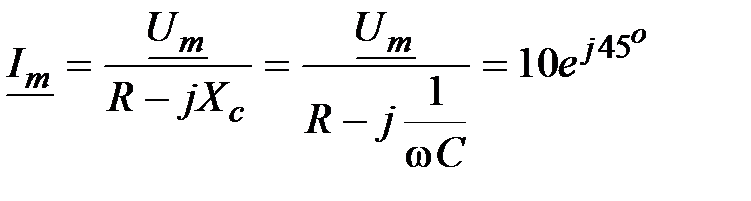 , А. , А.
| |
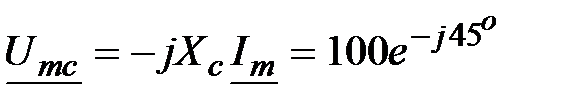 , В. , В.
| Отсюда 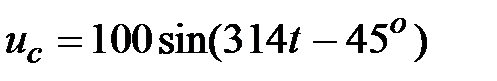 , В. , В.
|
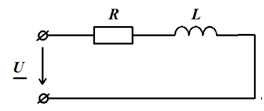
Задача 3.5. Дана цепь 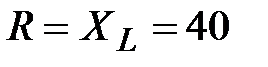 Ом,
Ом, 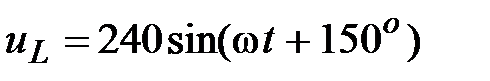 , В.
, В.
Определить 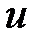 .
.
| Решение: На основе закона Ома: | 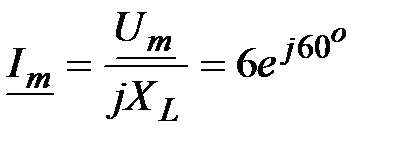 , А. , А.
| |
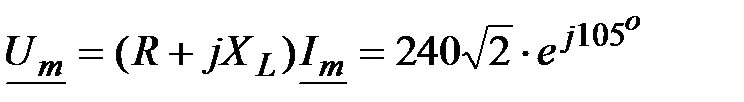 , В.
Отсюда , В.
Отсюда 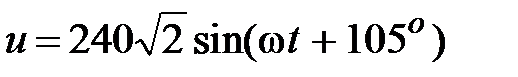 , В. , В.
| 
| |
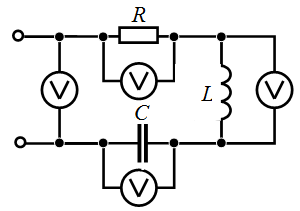
Задача 3.6 В цепи синусоидального тока все четыре вольтметра показывают одно и то же напряжение - 
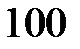 В. Определить
В. Определить 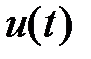 , если принять
, если принять 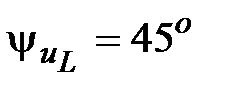 .
.
Решение: Так как 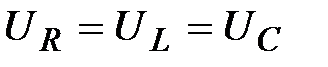 , то , то 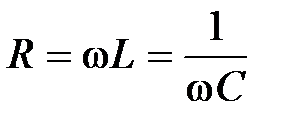 (в цепи резонанс напряжений).
Отсюда : (в цепи резонанс напряжений).
Отсюда : 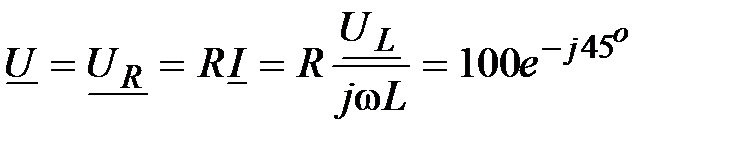 , В; , В;
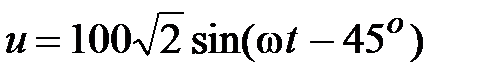 , В. , В.
| 
|
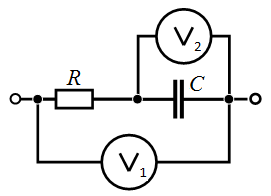
Задача 3.7 Какое показание вольтметра 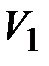 , в цепи синусоидального тока, если вольтметр
, в цепи синусоидального тока, если вольтметр 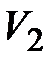 показывает
показывает 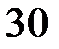 В,
В, 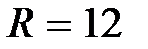 Ом,
Ом, 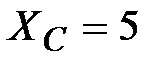 Ом.
Ом.
Решение: 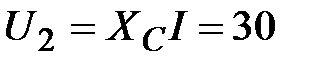 В, В, 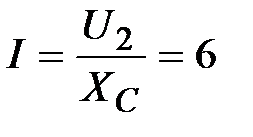 А.
Отсюда А.
Отсюда 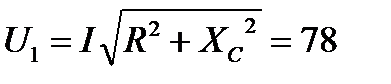 В. В.
| 
|
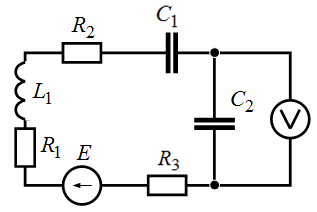
Задача 3.8 Найти показания вольтметра, если 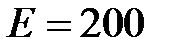 В,
В, 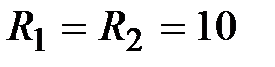 Ом,
Ом, 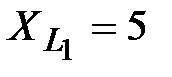 Ом,
Ом, 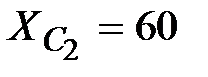 Ом,
Ом, 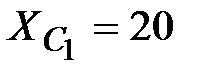 Ом,
Ом, 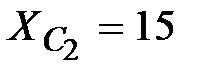 Ом.
Ом.
Решение: Вольтметр показывает действующее значение напряжения
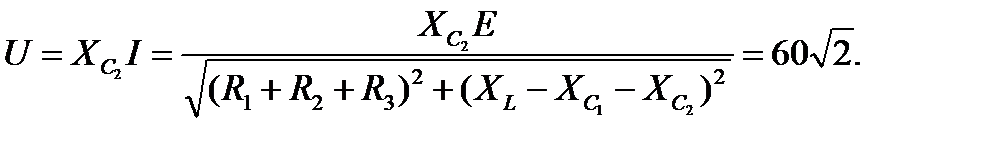
| 
|
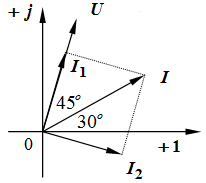
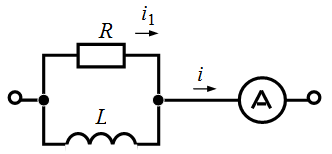
Задача 3.9 В цепи 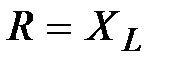 , амперметр показывает , амперметр показывает 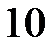 А.
Определить А.
Определить 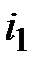 , если принять , если принять 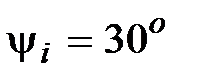 .
Решение: Из векторной диаграммы находим: .
Решение: Из векторной диаграммы находим:
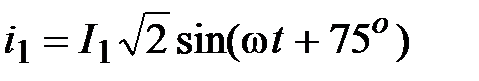 , А, , А,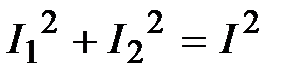 . .
| 
|
Так как 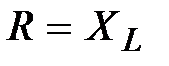 , то , то 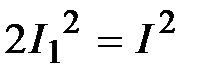 , , 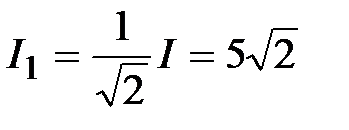 А.
Отсюда А.
Отсюда 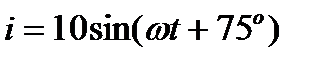 , А. , А.
| 
|
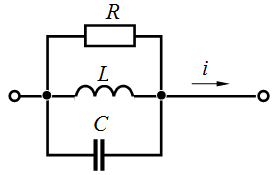
Задача 3.10 Найти 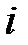 , если
, если 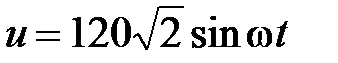 , В,
, В, 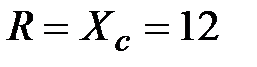 Ом,
Ом, 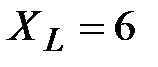 Ом.
Ом.
Решение: 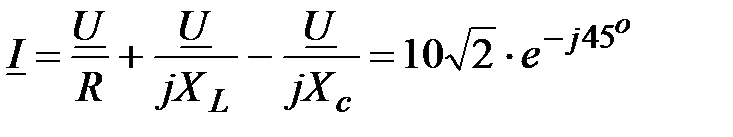 , А.
Отсюда , А.
Отсюда 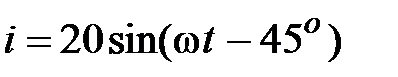 , А. , А.
| 
|
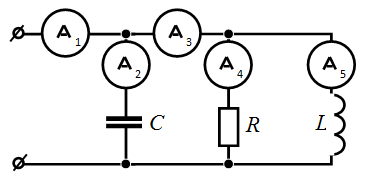
Задача 3.11 Определить показания амперметра 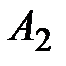 , если показания
, если показания
приборов 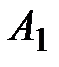 ,
, 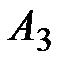 ,
, 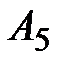 соответственно равны :
соответственно равны : 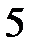 А,
А, 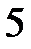 А,
А,  А.
А.
| 
|
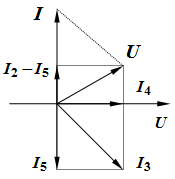
Решение: Из векторной диаграммы
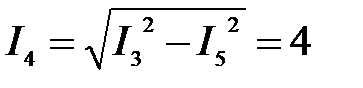 А, А, 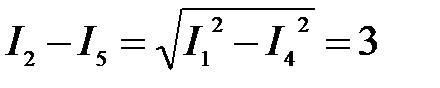 А. Отсюда А. Отсюда 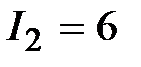 А. А.
|
Задача 3.12 Определить параметры (L, R) катушки, используя результаты двух опытов:
1) При включении катушки в сеть постоянного тока U = 200 В, в катушке ток I = 5 А.
2) При включении катушки в сеть переменного тока U = 200 В, 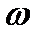 = 300 рад/сек., в катушке ток I = 4 А.
= 300 рад/сек., в катушке ток I = 4 А.
Решение: Используя результаты 1-го опыта, получим 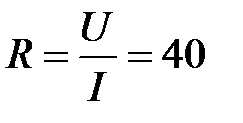 Ом.
Ом.
Используя результаты 2-го опыта, получим 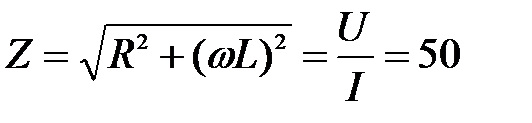 Ом.
Ом.
Отсюда: 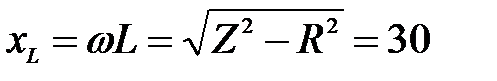 Ом;
Ом; 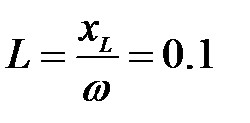 Гн.
Гн.
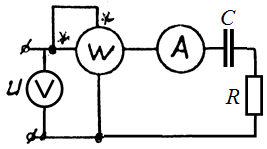
Задача 3.13 Определить Хc, если U=200 В, ваттмер показывает 480 Вт, амперметр 4 А.
Решение: Ваттметр показывает активную мощность 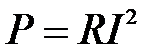 . Отсюда . Отсюда 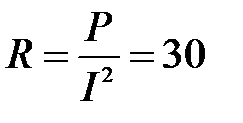 Ом.
Определив полное сопротивление цепи Ом.
Определив полное сопротивление цепи 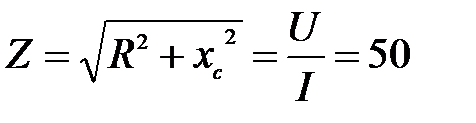 Ом.
Находим Ом.
Находим 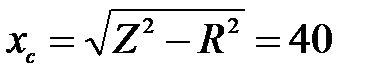 Ом. Ом.
| 
|
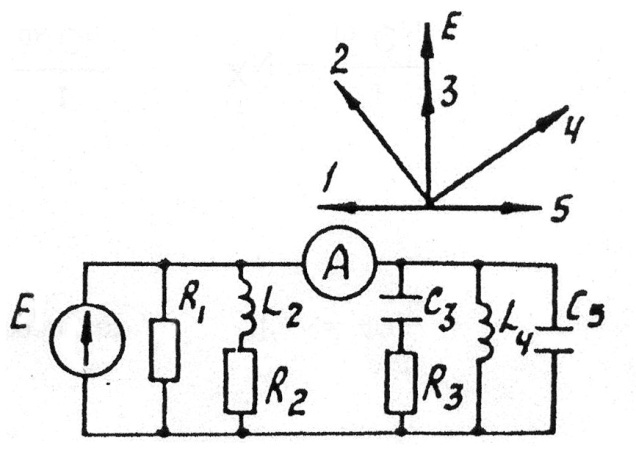
Задача 3.14 Дана схема и векторная диаграмма токов в параллельных ветвях. Какие вектора надо сложить, чтобы получить показание амперметра?
Решение: Амперметр покажет сумму токов: 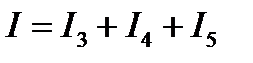 .
На векторной диаграмме току .
На векторной диаграмме току 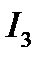 соответствует вектор 2, току
соответствует вектор 2, току 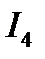 - вектор 5, току - вектор 5, току  - вектор 1.
Следовательно, для получения показания амперметра необходимо сложить 1, 2 и 5 вектора. - вектор 1.
Следовательно, для получения показания амперметра необходимо сложить 1, 2 и 5 вектора.
| 
|
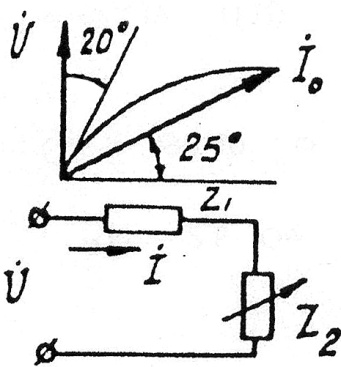
Задача 3.15 По круговой диаграмме определить аргументы сопротивлений Z1 и Z2.
Решение: 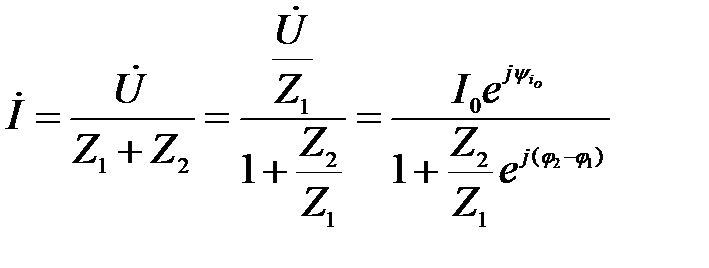 ;
Если: ;
Если: 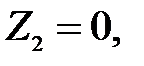 то то 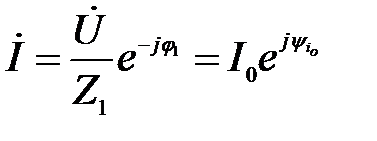 ;
Отсюда: ;
Отсюда: 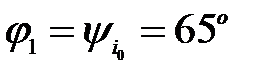 ;
Если : ;
Если : 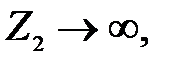 то то 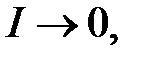 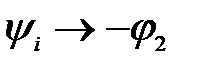 ;
Отсюда: ;
Отсюда: 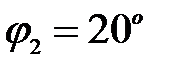
| 
|
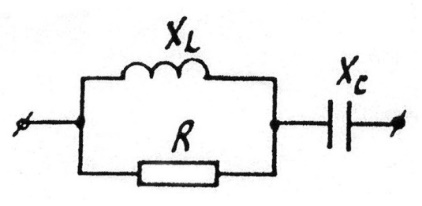
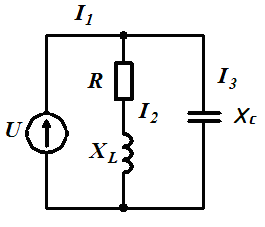
Задача 3.16 При каком значении xc в цепи возникает резонанс напряжений, если R = ХL = 4 Ом.
Решение: Условие резонанса: 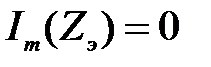
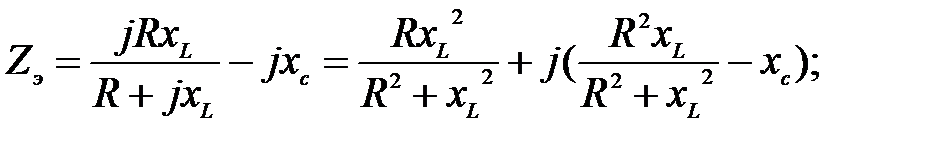 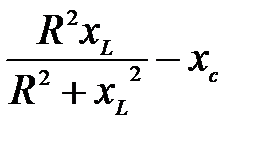 =0.
Отсюда xc=2 Ом. =0.
Отсюда xc=2 Ом.
| 
|
Задача 3.17 В цепи со следующими параметрами резонанс 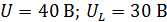 ;
; 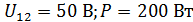 . Определить R,
. Определить R, 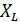 ,
, 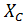 .
.
Решение:
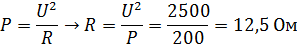 . .
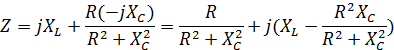 . .
| 
| ||||||
| Условие резонан-са | 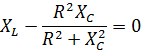
| Из условия резонанса следует, | 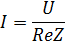
| С другой стороны | 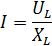
| ||
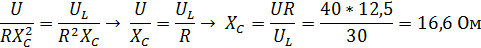 . .
| 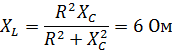 . .
| ||||||
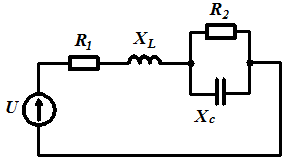
Задача 3.18 В заданной цепи: 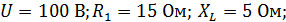
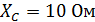 . Определить при каком значении
. Определить при каком значении 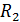 в цепи будет резонанс, и найти ток при резонансе.
в цепи будет резонанс, и найти ток при резонансе.
Решение:
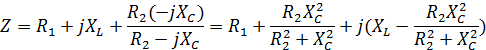
| 
| ||||
| Условие резонанса | 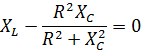
| Из этого уравнения получаем
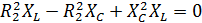
| 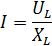
| ||
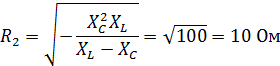
| Ток при резонансе | 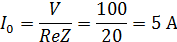
| |||
Задача 3.19 Определить сопротивления элементов цепи, если в цепи резонанс и P = 80 Вт; 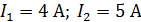 .
.
Решение:
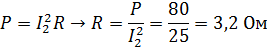
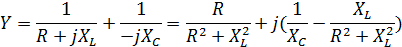
| 
| ||||||
| Условие резонан-са | 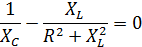
| Из условия резонанса следует, | 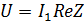
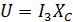
| Следовательно
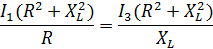
| |||
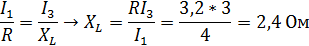
| 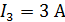
| 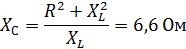 . .
| |||||
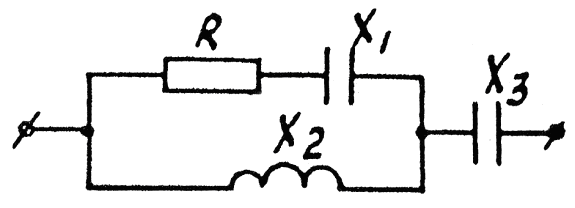
Задача 3.20 Определить R, при котором возникает резонанс токов, если x1=2 Ом, x2=4 Ом, x3=5 Ом
Решение: Условие резонанса: 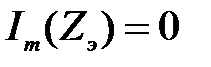
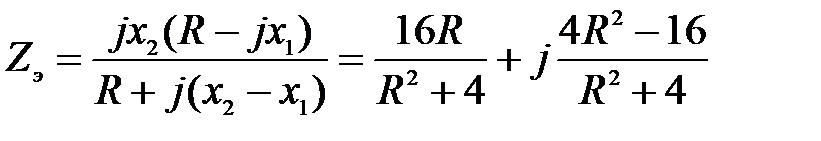 ; ; 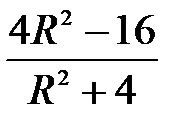 =0;
Отсюда R=2 Ом. =0;
Отсюда R=2 Ом.
| 
|
Задача 3.21
При каком значении 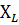 ток через резистор R будет максимальным, если ток через резистор R будет максимальным, если 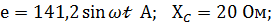 R=100 Ом. Определить токи во всех ветвях. R=100 Ом. Определить токи во всех ветвях.
| |
Решение. Максимальный ток будет в режиме согласованной нагрузки. Преобразуем источник Э.Д.С. Е в источник тока 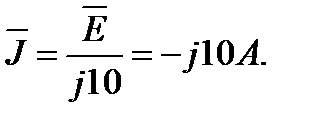 Максимальный ток будет при резонансе т.е.
Максимальный ток будет при резонансе т.е. 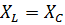 ,тогда ,тогда 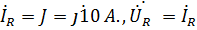 R=j10*100=j1000 A. R=j10*100=j1000 A. 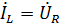 /j /j 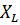 =50 A.Ток ветви источника Э.Д.С E с емкостью =50 A.Ток ветви источника Э.Д.С E с емкостью 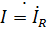 + + 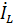 =50+j10 A. =50+j10 A.
| |
Задача 3.22 Реактор и конденсатор соединены последовательно. Найти напряжение на реакторе при резонансе, если входное напряжение равно 50 В, R=25 Ом, L=360 мГн, C=100 мкф.
Решение:
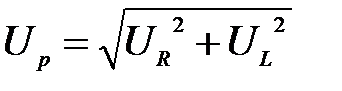 ;
; 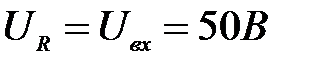 ;
; 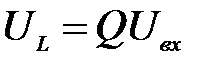 ;
; 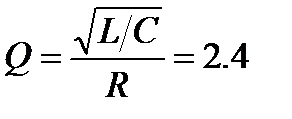 ;
; 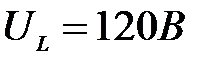
Отсюда 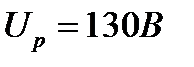
Задача 3.23 Максимальное и минимальное значение эквивалентной индуктивности последовательно соединённых одинаковых катушек равны соответственно 12 мГн и 6 мГн. Определить коэффициент связи.
Решение:
При согласном включении 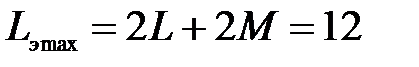 мГн.
мГн.
При встречном включении 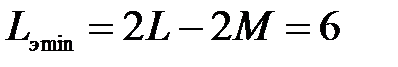 мГн.
мГн.
Отсюда: 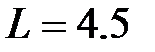 мГн,
мГн, 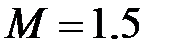 мГн,
мГн, 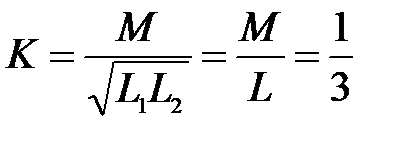
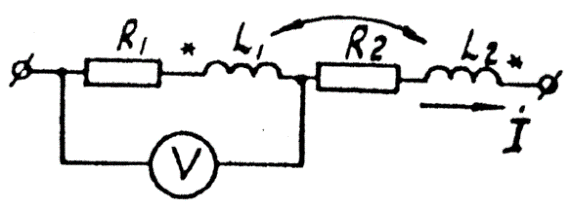
Задача 3.24 Найти 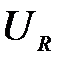 , если вольтметр показывает 100 В, а
, если вольтметр показывает 100 В, а 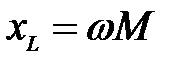
Решение:
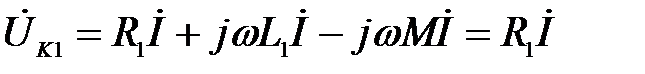 (так как
(так как 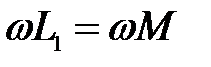 по условию)
Отсюда: по условию)
Отсюда: 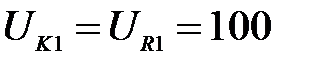 В В
| 
|
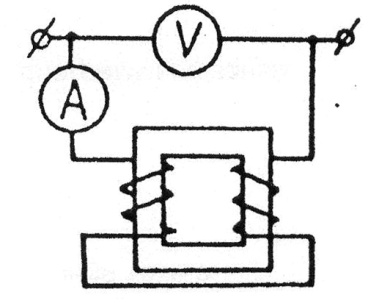
Задача 3.25 Определить показание вольтметра, если амперметр
показывает 5 А. Катушки одинаковые 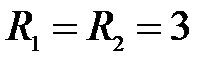 Ом,
Ом, 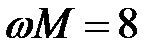 Ом, а
Ом, а
коэффициент связи равен единице.
Решение: По условию 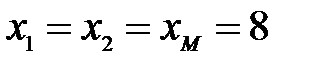 Ом
Используя правило буравчика, определяем, что катушки включены встречно.
Отсюда: Ом
Используя правило буравчика, определяем, что катушки включены встречно.
Отсюда: 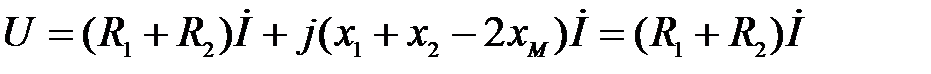 .
Показание вольтметра: .
Показание вольтметра: 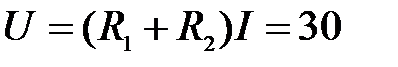 В. В.
| 
|
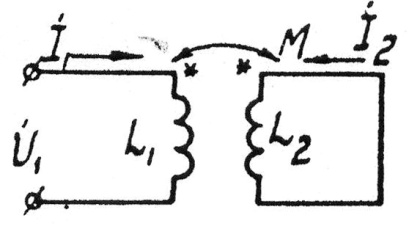
Задача 3.26 Выразить комплекс тока 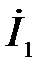 , через
, через 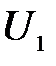 ;
; 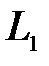 ;
; 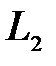 ;
; 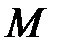 ;
; 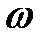 .
.
Активными сопротивлениями катушек пренебречь.
Решение:
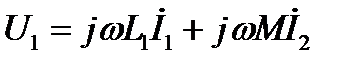 (1) (1)
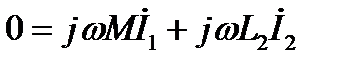 (2) (2)
| Решая уравнения (1) и (2) совместно, получим: 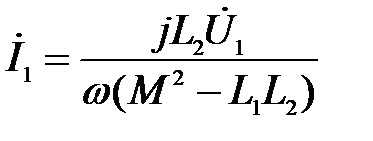
| 
|
Задача 3.26а.
Заданы  Записать уравнения цепи и определить входное сопротивление
Записать уравнения цепи и определить входное сопротивление  Решение:
Решение:
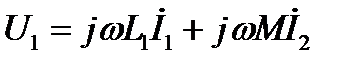 (1) (1)
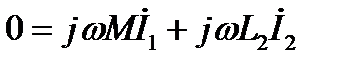 + + 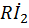 (2) (2) 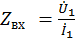
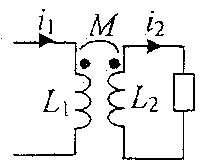
| 
|
Задача 3. 27 Определить входное сопротивление цепи, показанной на рис. Дано: 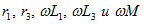 Решение. Зададимся напряжением Решение. Зададимся напряжением 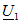 определим ток определим ток 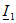 и затем найдем и затем найдем 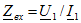 . Заметим, что если бы не было взаимной индуктивности, то . Заметим, что если бы не было взаимной индуктивности, то 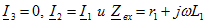 . Для контура 1-3-2-2'-1' . Для контура 1-3-2-2'-1' 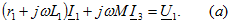 Для контура 3-3'-2'-2-3 Для контура 3-3'-2'-2-3 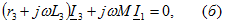 откуда откуда 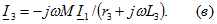 Подставив (в) в (а), получим откуда Подставив (в) в (а), получим откуда 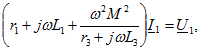 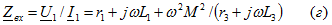
| |
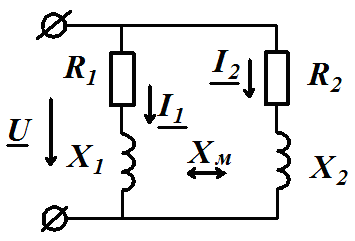
Задача 3.28 Определить токи 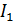 ,
, 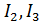 в ветвях цепи, если известно, что
в ветвях цепи, если известно, что 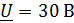 ;
; 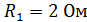 ;
; 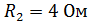 ;
; 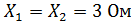 ;
; 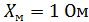 ;
;
Построить векторную топографическую диаграмму
Решение:
Уравнение цепи 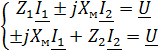 где
где 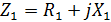 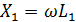 ; ; 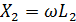 ; ; 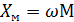
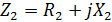 . .
| 
| |
| Верхний знак соответствуют согласному включению катушек. | ||
При встречном включении токи равны:
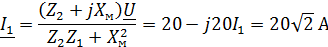
| 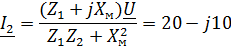
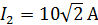
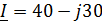 ; ; 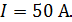
| |
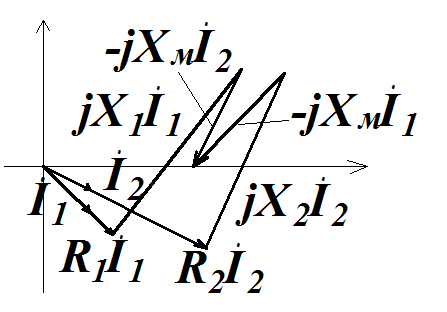
ВТД
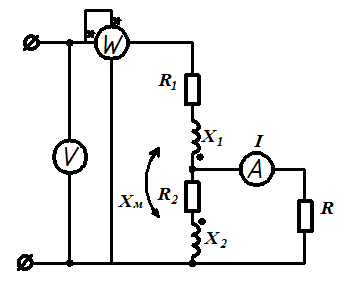
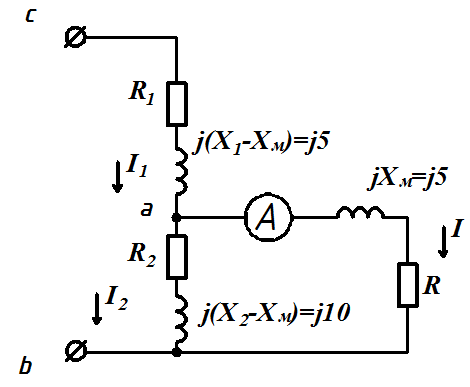
Задача 3.29 Определить показания V и P, если известно, что 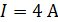 ;
; 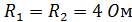 ;
; 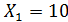 ;
; 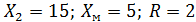
| Решение:
Схема замещения
|
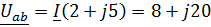
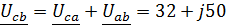
| 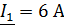 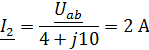
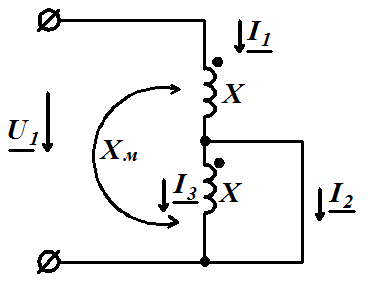
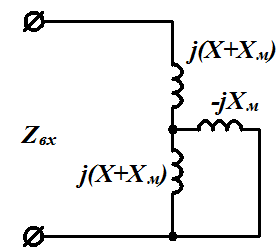
|
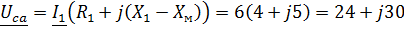
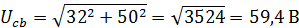
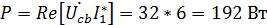
|
Задача 3.30 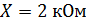 ;
; 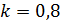 .Определить
.Определить 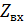 .
.
Решение: Первый способ:
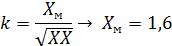
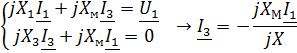
| 
| ||
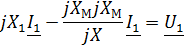
| 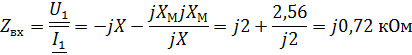
| ||
Второй способ: из схемы замещения
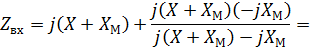
| 
| ||
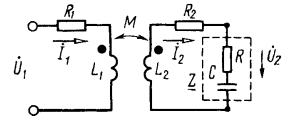
Задача 3.31. К первичной обмотке трансформатора подведено напряжение 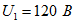 Определить напряжение на
сопротивлении Определить напряжение на
сопротивлении 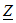 при при 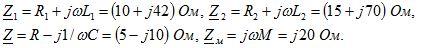 Решение: Система уравнений второго закона Кирхгофа для этого случая Решение: Система уравнений второго закона Кирхгофа для этого случая
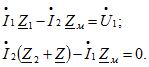 Отсюда Отсюда 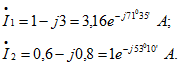 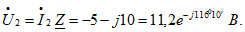
|
| ||
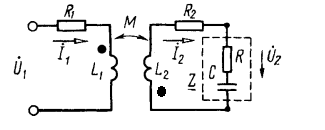
.Задача 3.32 К первичной обмотке трансформатора подведено напряжение 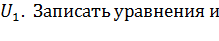 определить напряжение на сопротивлении определить напряжение на сопротивлении 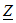 при согласном включении катушек
11 при согласном включении катушек
11 
| 
| ||
Задача 3.33. К выводам 1-1' цепи подведено питание. Определить напряжение между разомкнутыми выводами 2-2'. Дано: 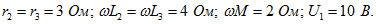 Решение. Полагаем Решение. Полагаем 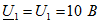 . Находим: . Находим: 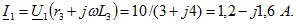 Напряжение Напряжение 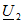 определяем, обходя схему от вывода 2 к выводу 2': определяем, обходя схему от вывода 2 к выводу 2': 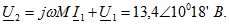
| |
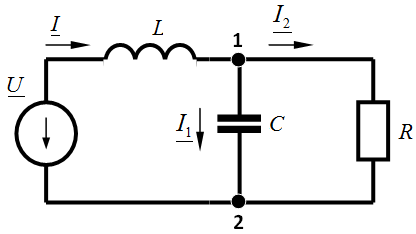
Задача 3.34 Определить токи в ветвях и составить уравнение баланса мощностей цепи. 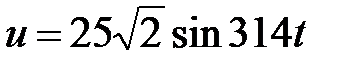 , В,
, В, 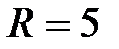 Ом,
Ом, 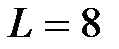 мГн,
мГн, 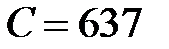 мкФ.
мкФ.
Решение: На основе закона Ома 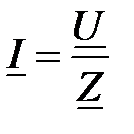 ; ; 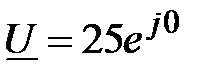 , В, , В,
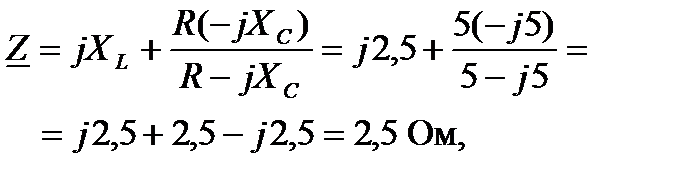 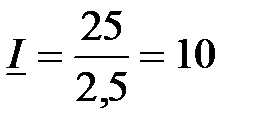 А; А;
| 
|
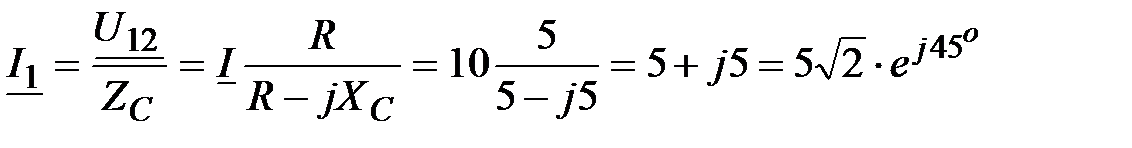 , А;
, А; 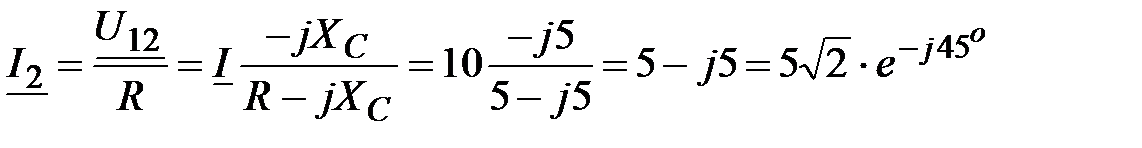 , А.
, А.
Уравнение баланса мощностей :
мощность источника 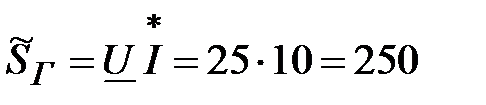 ;
;
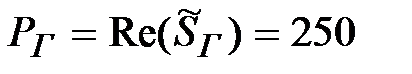 Вт,
Вт, 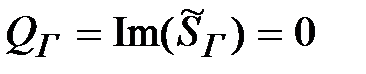 ;
;
мощность приемников:
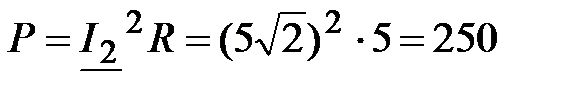 Вт;
Вт;
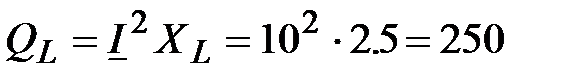 вар;
вар;
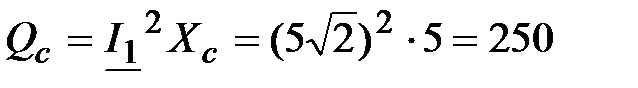 вар;
вар;
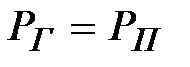 ,
, 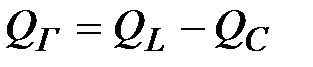 ;
;
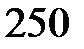 Вт =
Вт = 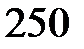 Вт,
Вт, 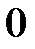 вар =
вар = 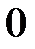 вар.
вар.
Задача 3.35 Определить токи в ветвях и составить уравнение баланса мощностей.
Решение: 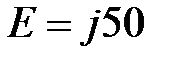 , В, , В, 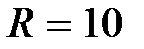 Ом, Ом, 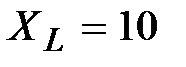 Ом, Ом,
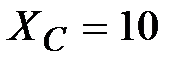 Ом
Ответ: Ом
Ответ: 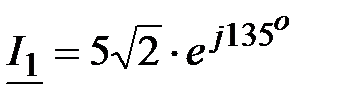 , А, , А, 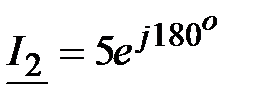 ,А, ,А, 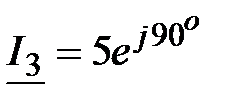 , А , А
| 
|
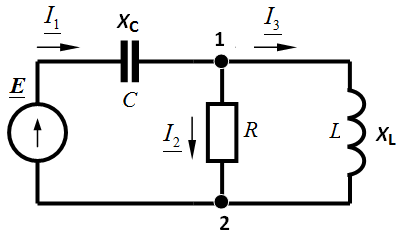
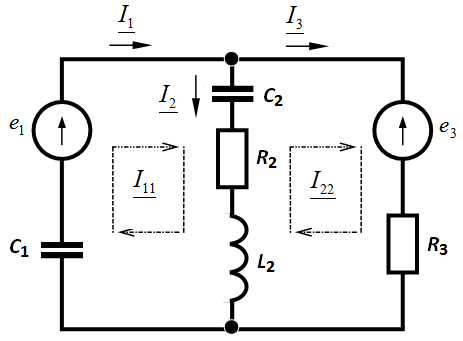
Задача 3.36. Определить токи в ветвях методом законов Кирхгофа.
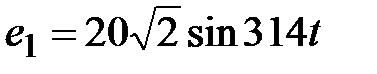 , В; , В;
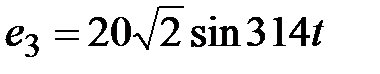 , В; , В;
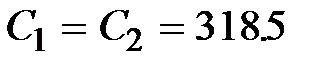 ,мкФ; ,мкФ;
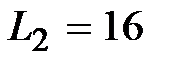 мГн, мГн, 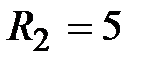 Ом, Ом,
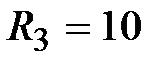 Ом. Ом.
| 
|
Решение:
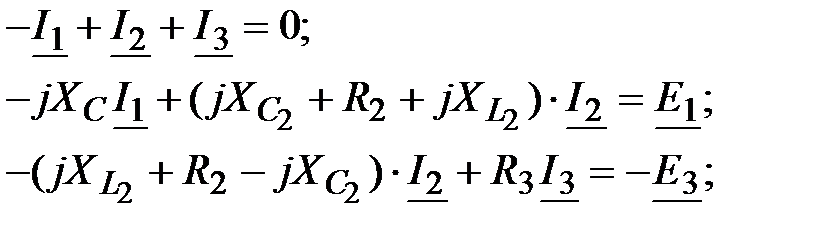
| 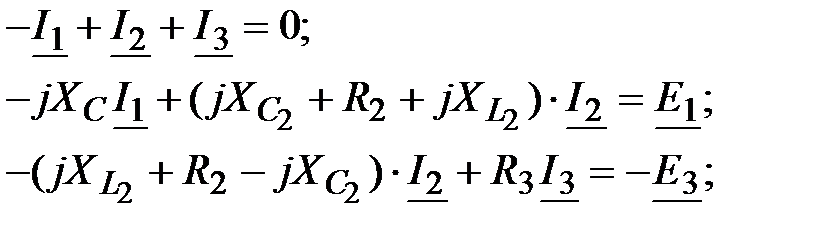
|
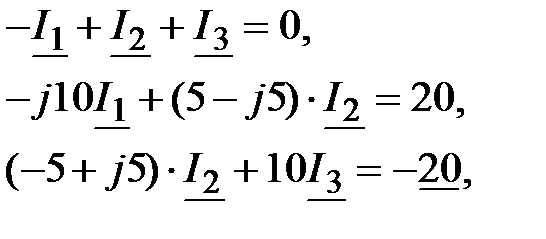
| 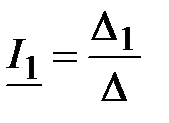 , , 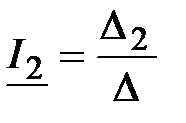 , , 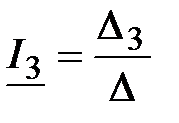 ; ;
|
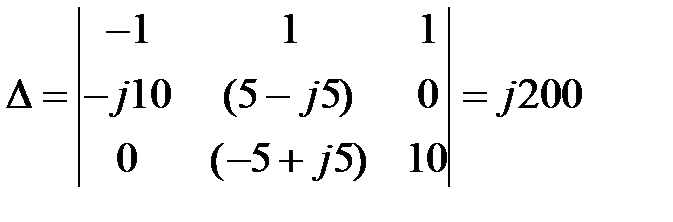
| 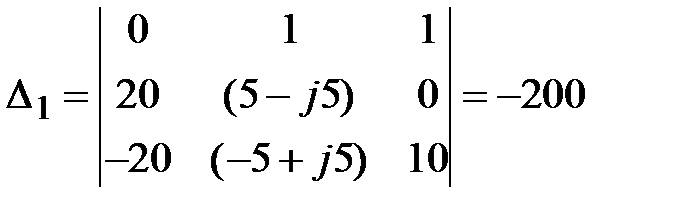
|
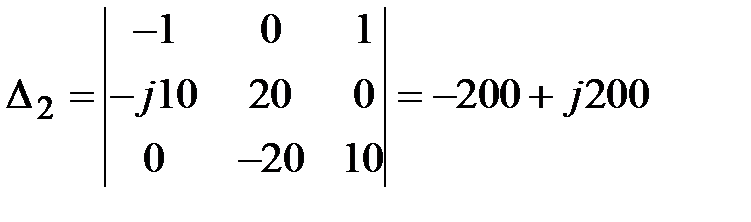
| 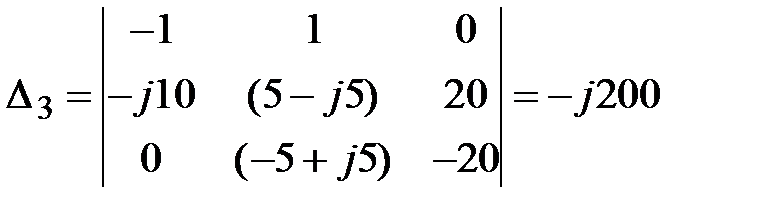
|
Значения токов в ветвях
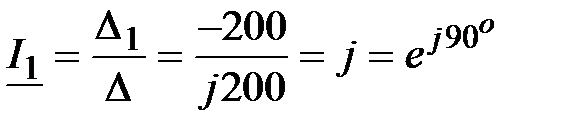 , А, , А,
| 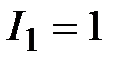 А, А, 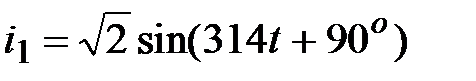 , А; , А;
|
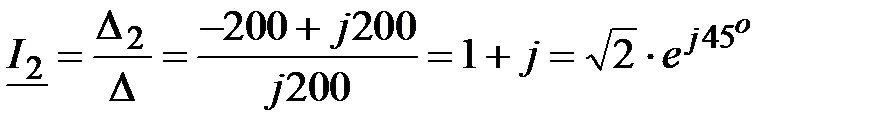
| 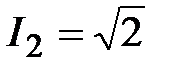 А, А,
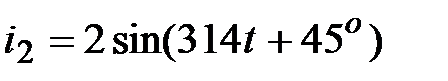 , А; , А;
|
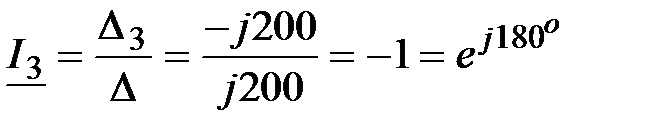 , А, , А,
| 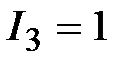 А, А, 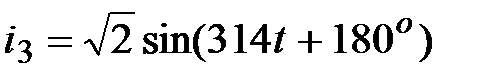 ,А; ,А;
|
Баланс мощностей:
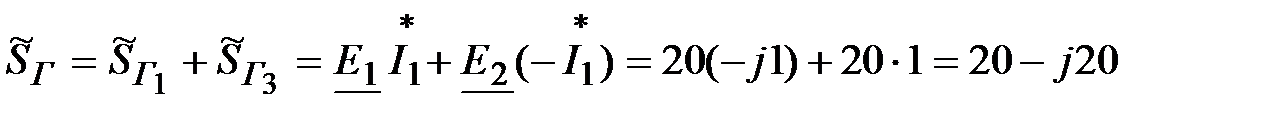 ;
;
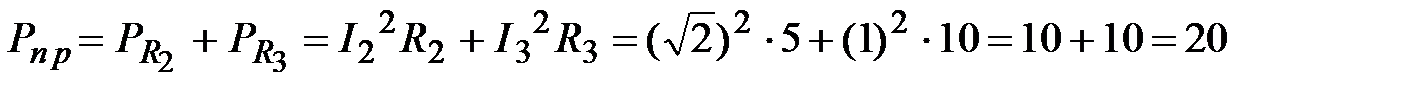 Вт;
Вт;
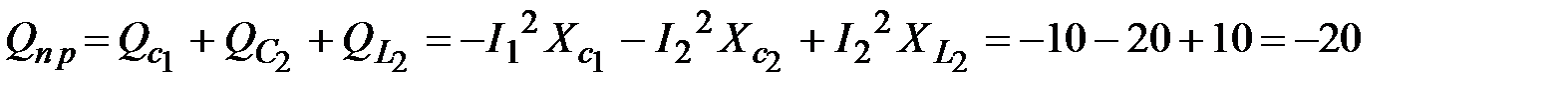 Вт;
Вт;
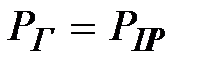 , ,
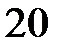 Вт = Вт = 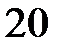 Вт, Вт,
| 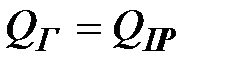 ; ;
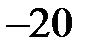 вар = вар = 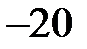 вар. вар.
|
Задача 3.37. Решить предыдущую задачу методом контурных токов.
Решение:
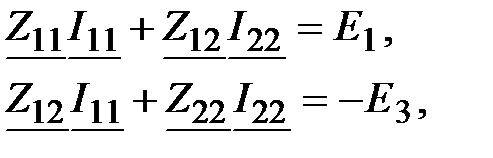 где где
| 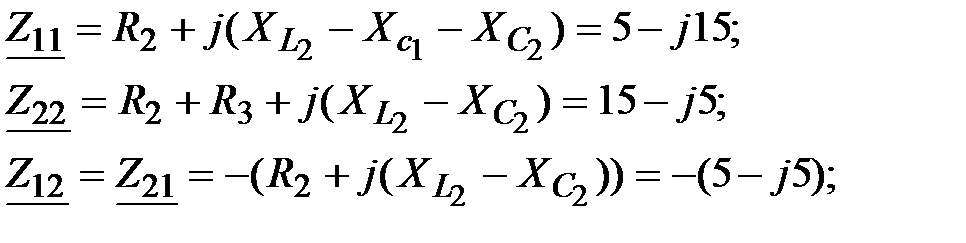
| |
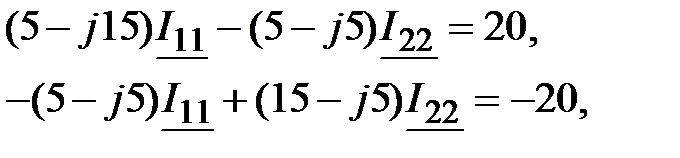
| 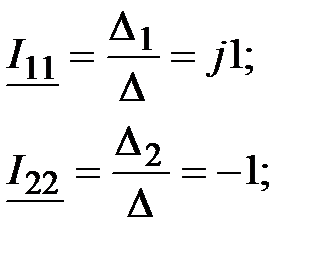
| 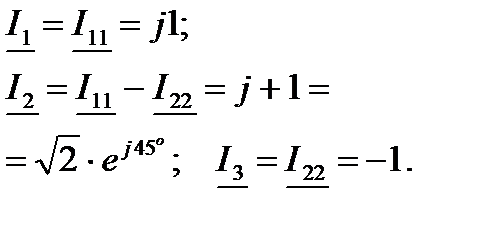
|
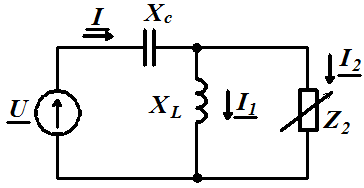
Задача 3.38. Дана цепь. При каком соотношении между 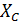 и
и 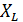 ток
ток 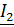 не будет зависеть от
не будет зависеть от 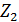 .
.
Решение: Уравнения цепи по закону Кирхгофа
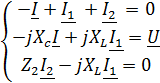
| 
|
Из уравнения найдем, что 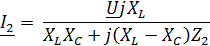
| Ток 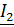 не будет зависеть от не будет зависеть от 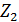 , если , если 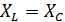
| Тогда
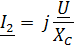
|
Задача 3.39 В левой схеме задан ток ветви 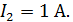 Определить
Определить 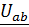 и построить В.Т.Д.
и построить В.Т.Д.
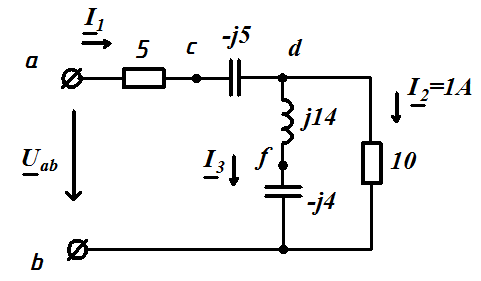
| В.Т.Д.
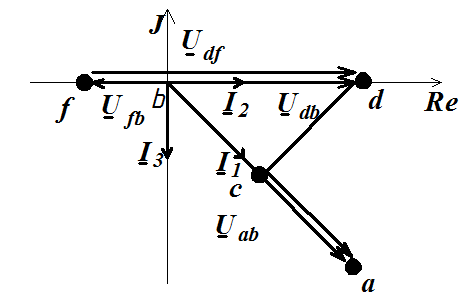
|
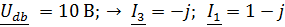
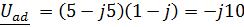
| 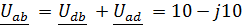
|
Задача 3.40. 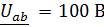 ;
; 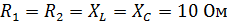 . Определить
. Определить 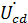 и построить В.Т.Д.
и построить В.Т.Д.
 Решение:
Решение:
| В.Т.Д.
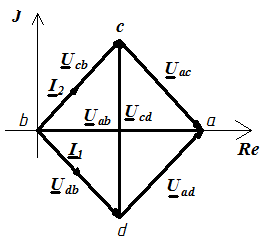
|
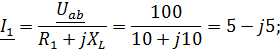
| 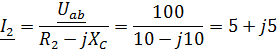
|
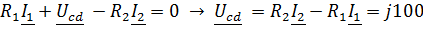
|
Задача 3.41 Определить 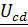 в предыдущей задаче, если во второй ветви поменять местами
в предыдущей задаче, если во второй ветви поменять местами 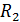 и
и 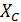
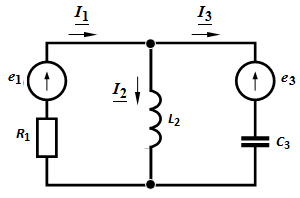
Задача 3.42 Определить токи в ветвях цепи методом наложения
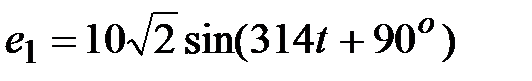 , В; , В;
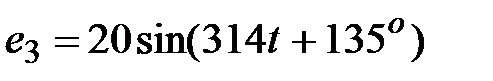 , В , В
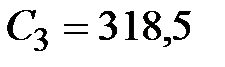 мкФ, мкФ, 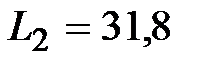 мГн, мГн, 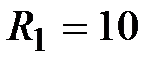 Ом.
Ответ: Ом.
Ответ:
| 
| ||
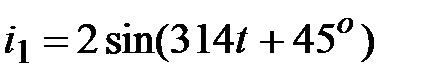 , А; , А;
| 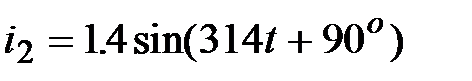 , А; , А;
| 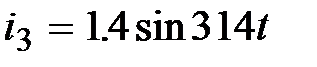 , А. , А.
| |
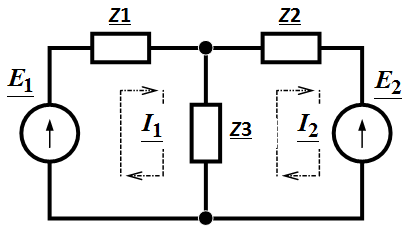
Задача 3.43 Определить 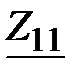 и
и 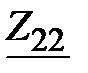 , если
, если 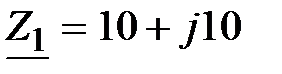 Ом,
Ом, 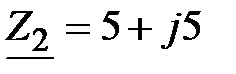 Ом,
Ом, 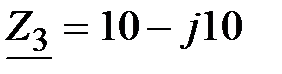 Ом.
Ом.
Решение: Собственное сопротивление
первого контура
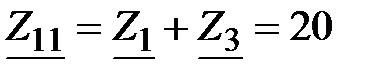 Ом.
Взаимное сопротивление контуров Ом.
Взаимное сопротивление контуров
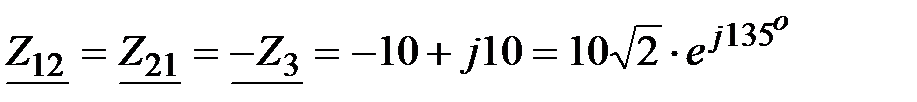 , Ом. , Ом.
| 
|
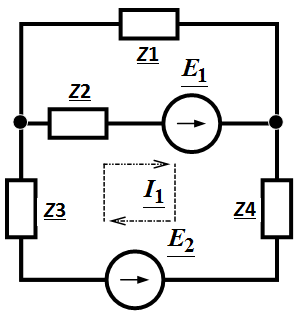
Задача 3 .44. Определить 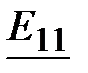 , если , если
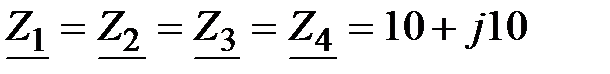 Ом; Ом;
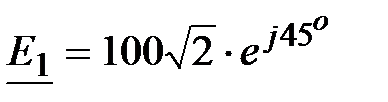 , В, , В, 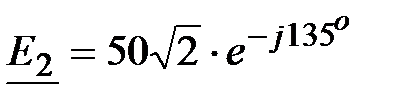 , В.
Решение: Собственная ЭДС контура , В.
Решение: Собственная ЭДС контура
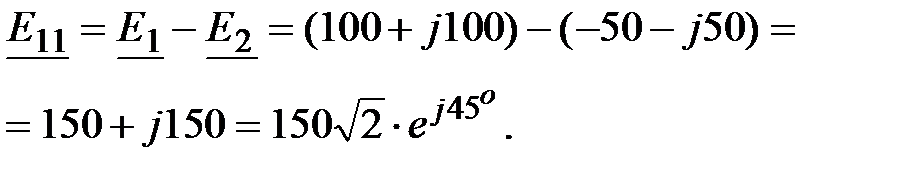
| 
|
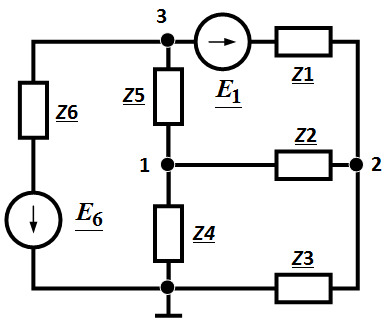
Задача 3.45 Определить 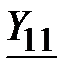 и
и 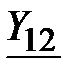 , если
, если 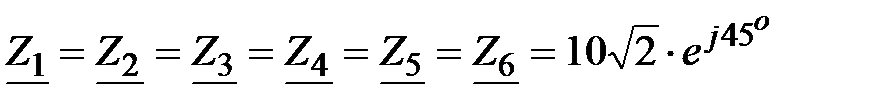 , Ом.
, Ом.
Решение: Собственная проводимость
первого узла
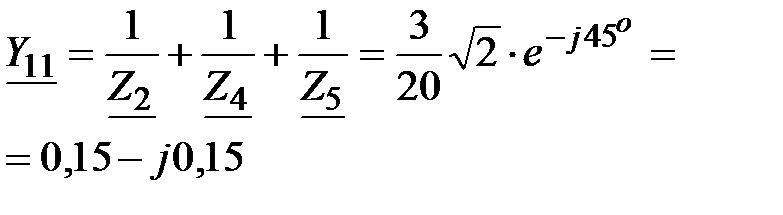 Взаимная проводимость
Взаимная проводимость
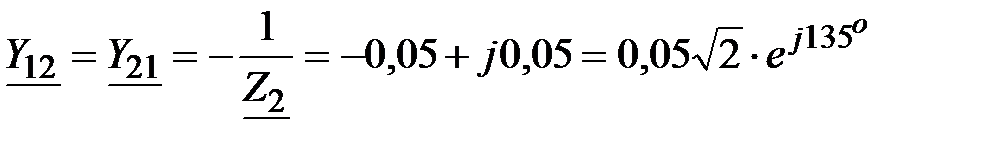 . .
| 
|
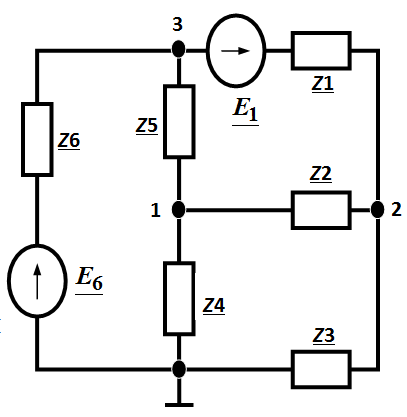
Задача 3.46. Определить 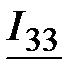 , если , если 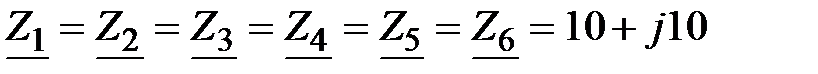 Ом; Ом;
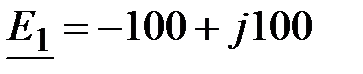 , В; , В; 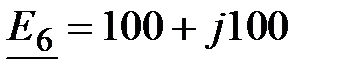 , В.
Решение: Собственный ток третьего узла , В.
Решение: Собственный ток третьего узла
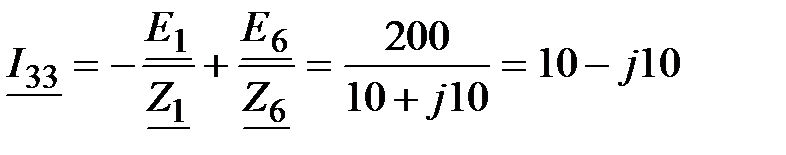 , А. , А.
| 
|
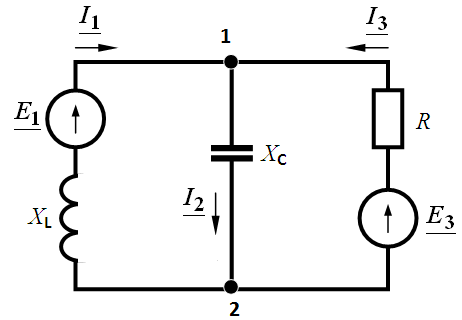
Задача 3.47. Решить задачу методом двух узлов. 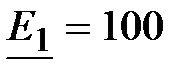 В,
В, 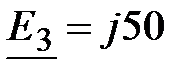 , В,
, В, 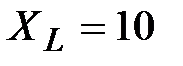 Ом,
Ом, 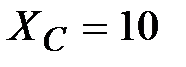 Ом,
Ом, 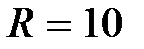 Ом.
Ом.
Решение:
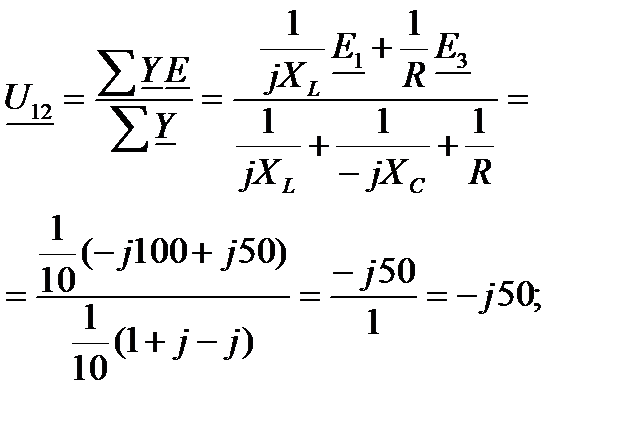
| 
| ||
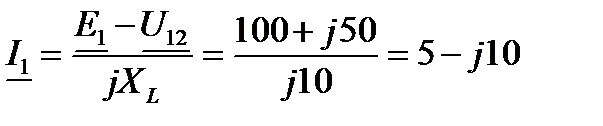 . .
| 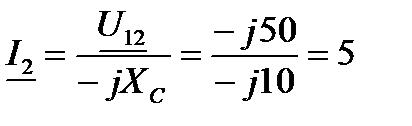 . .
| 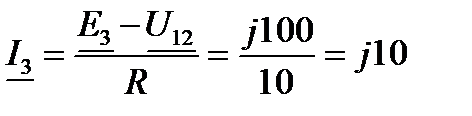 . .
| |
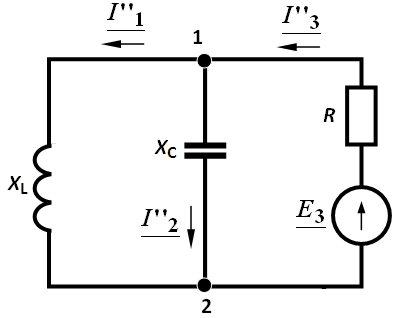
Задача 3.48. Решить предыдущую задачу методом наложения.
Решение: 1. Расчет токов в цепи от действия 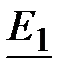
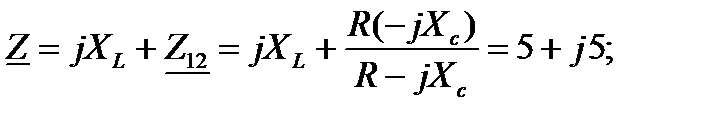
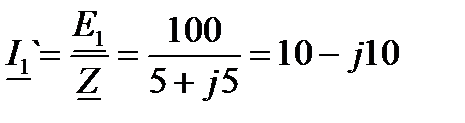 . .
| 
| |||
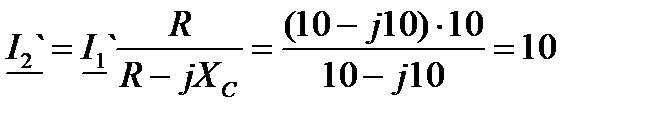 . .
| 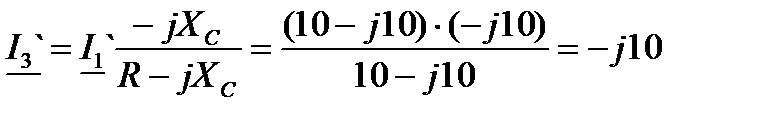 . .
| |||
Решение: 2. Расчет токов в цепи от действия 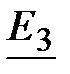
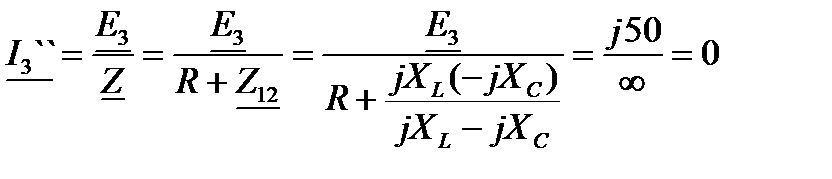 , А; , А;
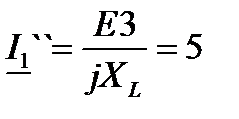 , А; , А;
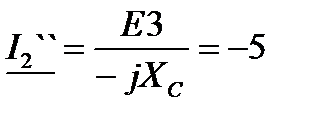 , А. , А.
| 
| |||
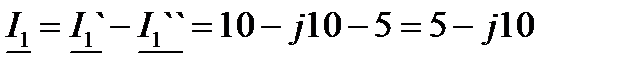 . .
| 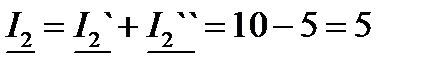 . .
| 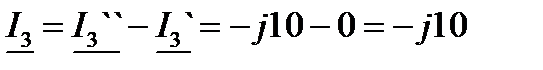 . .
| ||
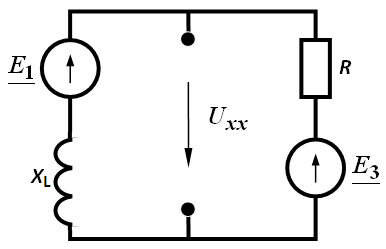
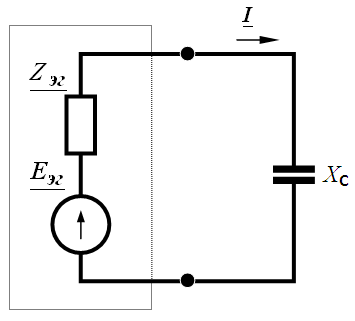
Задача 3.49 Определить ток в 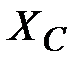 методом эквивалентного генератора. (Схема задачи 3.48).
методом эквивалентного генератора. (Схема задачи 3.48).
Решение:
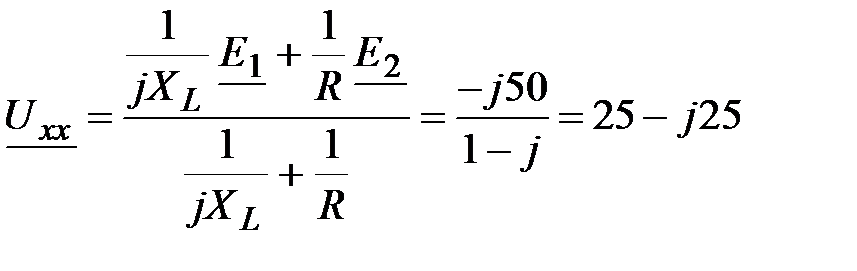 ; ;
| 
|
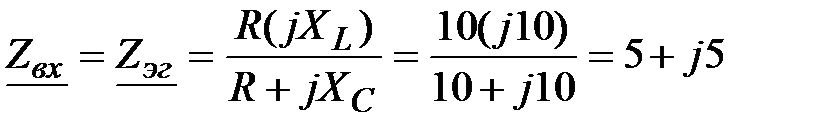 ; ;
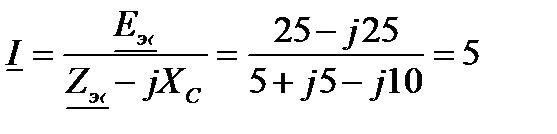 . .
| 
|
Задача 3.50. Определить 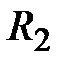 , при котором сдвиг фаз между
, при котором сдвиг фаз между 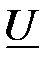 и
и 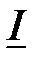 равен
равен 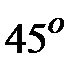 .
. 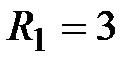 Ом,
Ом, 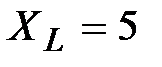 Ом.
Ом.
Решение: 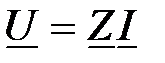 ;
; 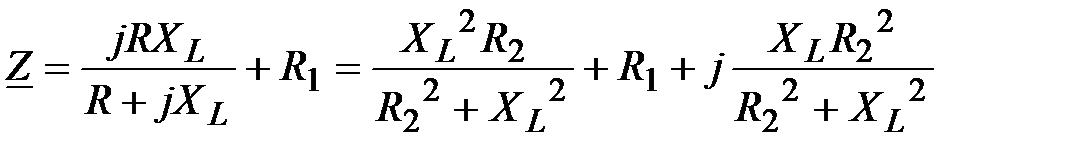 .
.
Чтобы сдвиг фаз был равен 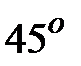 , необходимо, чтобы:
, необходимо, чтобы:
| R1 |
| R2 |
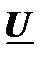
|
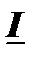
|
| X |
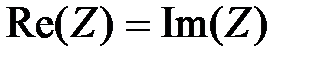 или
или
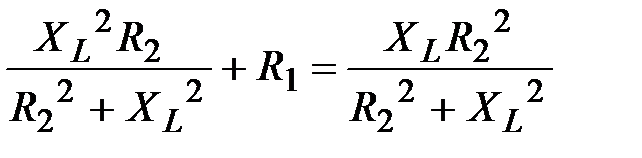 .
.
Отсюда получаем уравнение:
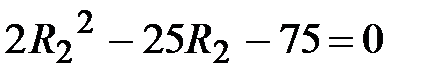 ,
,
решая которое находим 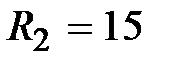 Ом.
Ом.
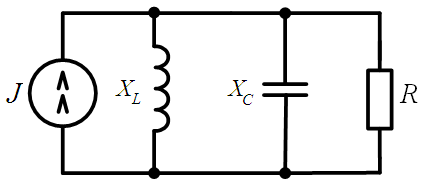
Задача 3.51.
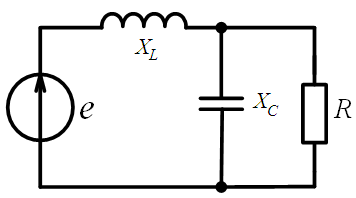
При каком значении 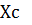 активная мощность в R будет максимальная, если
активная мощность в R будет максимальная, если 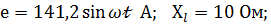 R=50 Ом.
R=50 Ом.
Решение: Источник ЭДС с 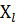 заменяем эквивалентной схемой замещения, где заменяем эквивалентной схемой замещения, где 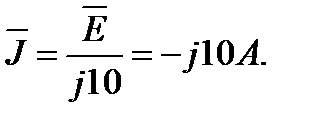
| 
|
Максимальная мощность имеет место при резонансе токов при 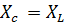 .
Ответ: Р= .
Ответ: Р= 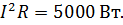
| 
|
Дата добавления: 2021-12-14; просмотров: 1025;











