Самостоятельная работа

Задание. Расчет цепей по комплексным значениям

На рисунке 1 приведена схема электрической цепи, состоящая из шести обобщенных ветвей, каждая из которых содержит источник тока J, источник напряжения E, и комплексное сопротивление Z. Используя данные таблицы 1 и 2, составить расчетную схему, соответствующую заданному варианту. Применяя метод контурных токов для комплексных амплитуд, выполнить следующее:

1) определить амплитуды токов во всех ветвях схемы;

2) определить напряжения на всех элементах внешнего контура;

3) составить баланс активных и реактивных мощностей;

4) построить векторную диаграмму токов цепи;

5) построить векторную диаграмму для напряжений внешнего контура.

Параметры пассивных элементов схемы приведены в таблице 1 и параметры источников в таблице 2.

Рис. 1

Таблица 1

Параметры элементов цепи

Таблица 2

Параметры источников напряжения и тока

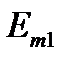
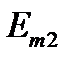
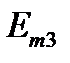
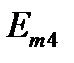
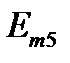
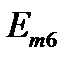
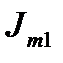
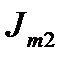
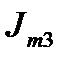
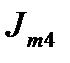
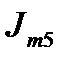
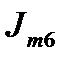
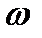
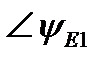
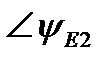
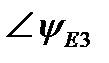
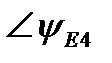
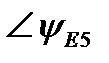
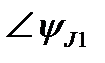
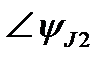
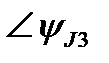
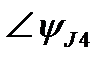
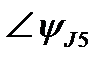
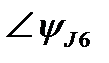
рад/с

14,5

5,5

∠0°

∠-55°

∠70°

16,5

4,25

∠-75°

∠0°

∠90°

18,5

3,75

∠85°

∠-25°

∠0°

20,5

∠0°

∠40°

∠-55°

22,5

1,5

∠60°

∠0°

∠-75°

5,25

∠-80°

∠10°

∠0°

4,75

∠0°

∠25°

∠-40°

∠45°

∠0°

∠-60°

24,5

5,5

∠80°

∠-10°

∠0°

∠0°

∠-10°

∠25°

19,5

5,75

∠30°

∠0°

∠-45°

21,5

∠50°

∠-65°

∠0°

4,5

∠75°

∠0°

∠-90°

10,5

∠-15°

∠0°

∠30°

12,5

1,5

∠-35°

∠50°

∠0°

∠0°

∠55°

∠-70°

23,5

3,5

∠0°

∠70°

∠-85°

∠-20°

∠35°

∠0°

2,5

∠0°

∠-40°

∠55°

1,25

∠-60°

∠0°

∠75°

2,5

∠65°

∠-80°

∠0°

11,5

∠0°

∠-25°

∠-40°

13,5

3,5

∠-45°

∠0°

∠60°

15,5

1,25

∠-65°

∠80°

∠0°

17,5

1,75

∠0°

∠-85°

∠15°

∠-30°

∠0°

∠45°

∠35°

∠-50°

∠0°

2,75

∠-90°

∠0°

∠20°

3,25

∠0°

∠-70°

∠85°

7,5

∠-50°

∠65°

∠0°

Приложения

Приложение 1

Резонансные режимы в цепи. Резонанс напряжения, резонанс

Токов

Реактивные сопротивления и проводимости отдельных участков цепи могут быть положительными (индуктивные элементы) и отрицательными (емкостные элементы). Поэтому возможны такие сочетания этих элементов, когда входное реактивное сопротивление или входная реактивная проводимость всей цепи равны нулю. При этом ток и напряжение на входе цепи совпадают по фазе и эквивалентное сопротивление всей цепи является активным. Такие режимы цепи называются резонансными.

Резонанс напряжений. На рис.2.7 приведена цепь, включающая последовательно соединенные активное сопротивление, индуктивность и емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда индуктивное и емкостное сопротивления одинаковы по величине (рис.2.10). Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонанса напряжения.

Ток в резонансном режиме достигает максимума, так как полное сопротивление z цепи имеет минимальное значение:

.

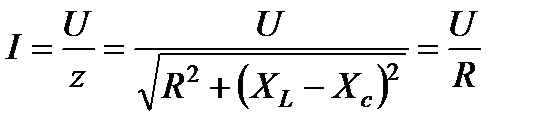Условие возникновения резонанса: .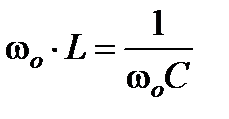

Частоту 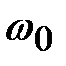называют резонансной частотой:

.

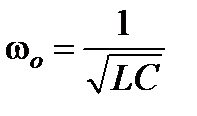В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, значительно превышающие напряжение на входе цепи, если реактивные сопротивления значительно превышают активное сопротивление. Напряжение на индуктивности при резонансе равно напряжению на емкости:

.

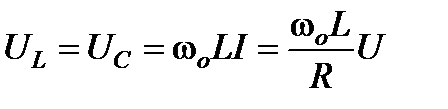Отношение 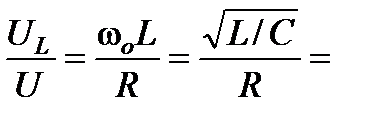Q называют добротностью контура.

Добротность показывает, во сколько раз напряжения на реактивных элементах превышают входное напряжение в резонансном режиме. В радиотехнических цепях добротность составляет несколько сотен. Резонансные свойства характеризуют также величиной обратной добротности 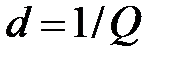, называемой затуханием контура.

Волновое сопротивление контура или характеристическое сопротивление 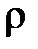определяет отношение напряжения на реактивных элементах в резонансном режиме к величине тока:

.

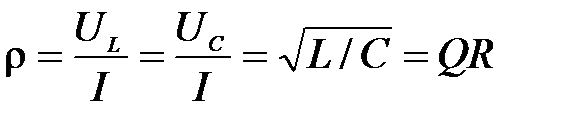Резонанс токов. На рис.2.11 приведена цепь, включающая параллельно соединенные активное сопротивление, идеальная индуктивность и емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда реактивная проводимость цепи 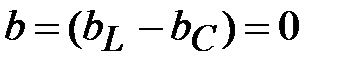(рис.2.14). При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением. В электрической цепи наступает режим резонанса токов.

Из условия возникновения резонанса тока получим формулу для резонансной частоты тока:

.

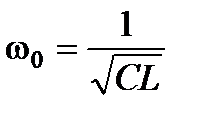В режиме резонанса тока полная (входная) проводимость цепи 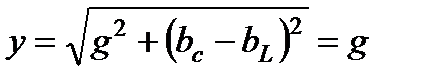- минимальна, а полное сопротивление 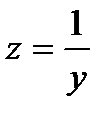- максимально. Ток в неразветвленной части схемы 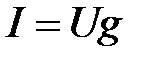в резонансном режиме имеет минимальное значение, в отличие от резонанса напряжений, когда ток имеет максимальное значение. В идеализированном случае при R = 0,

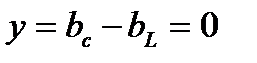и .

Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр - пробкой.

При резонансе токов возможны режимы, когда токи через индуктивность и емкость значительно превосходят ток в неразветвленной части схемы. Превышение токов в реактивных элементах над током в неразветвленной части схемы имеет место при условии

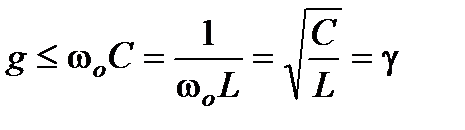
Величина 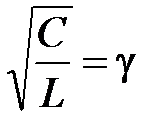имеет размер проводимости и называется волновой проводимостью контура.

Добротность контура Q при резонансе токов определяет кратность превышения тока в индуктивности 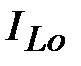и емкости 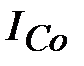над током в неразветвленной части схемы :

.

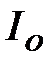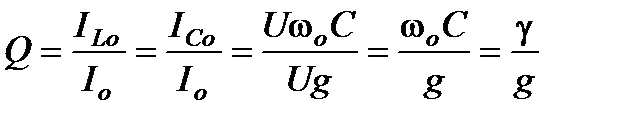Величина обратная добротности 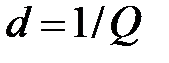является затуханием контура.

Важной характеристикой контура является его полоса пропускания

,

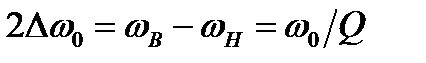которая характеризует избирательные свойства контура. Из этого выражения следует, что с повышением добротности контура его полоса пропускания уменьшается. Относительная полоса пропускания

,

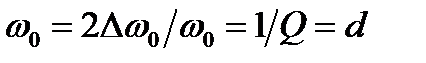где 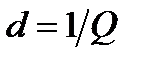— затухание контура.

Приложение 2

Расчет разветвленных цепей при наличии взаимной индуктивности

Расчет разветвленных цепей можно вести, составляя уравнения по первому и второму законам Кирхгофа или методом контурных токов. Метод узловых потенциалов непосредственно непригоден. Объясняется это тем, что ток в любой ветви зависит не только от ЭДС находящегося в ней источника и от потенциалов тех узлов, к которым ветвь присоединена, но и от токов других ветвей, которые наводят ЭДС взаимной индукции. Поэтому нельзя простым путем выразить токи ветвей через потенциалы узлов и ЭДС источников, как в цепях без индуктивно связанных элементов.
Применение метода узловых потенциалов требует особых приемов и здесь не рассматривается.
Принцип эквивалентного генератора можно применять, если внешняя по отношению к двухполюснику часть цепи не имеет индуктивных связей с той частью цепи, которая входит в состав двухполюсника. Разумеется, что нельзя пользоваться выведенными ранее формулами для преобразования треугольника сопротивлений в эквивалентную звезду и обратно.
Чтобы обойти указанные выше ограничения в применении расчетных методов, в ряде случаев целесообразно исключить индуктивные связи, перейдя к эквивалентным схемам без индуктивных связей (см. раздел развязывание индуктивных связей).
При составлении уравнения по второму закону Кирхгофа ЭДС взаимной индукции обычно учитываются как соответствующие напряжения. Знак комплексного напряжения 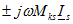на элементе k определяется на основании сопоставления направления обхода элемента к и положительного направления тока в элементе s. Если эти направления относительно одноименных выводов одинаковы, то напряжение равно 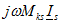. В противном случае напряжение равно 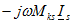. Это правило знаков вытекает из обоснований, приведенных в разделе.
В качестве примера запишем уравнения по законам Кирхгофа для схемы, представленной на рис. 6.10. Для большей ясности напряжения в уравнениях выпишем в порядке расположения элементов контура без приведения подобных членов:

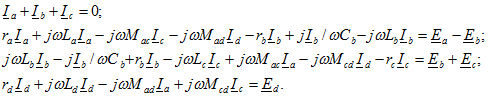
Приведем также уравнения, составленные по второму закону Кирхгофа для контурных токов:

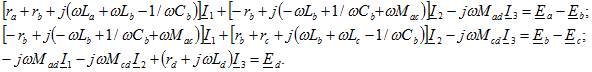
Сокращенно последние уравнения можно записать так:

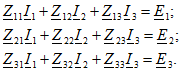
где 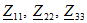- комплексные сопротивления контуров 1, 2 и 3;
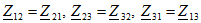- комплексные взаимные (общие) сопротивления контуров 1 и 2, 2 и 3, 3 и 1; 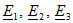- комплексные контурные ЭДС. Например,

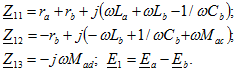
Заметим, что в комплексные сопротивления контуров и в комплексные взаимные сопротивления двух контуров слагаемые 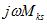входят со знаком плюс или минус в зависимости от того, совпадают или не совпадают по отношению к одноименным выводам элементов цепи k и s направление обхода контура через элемент к и положительное направление тока через элемент s.
Для цепей, содержащих индуктивно связанные элементы, справедливо свойство взаимности. Доказательство этого положения ничем не отличается от приведенного для цепей постоянного тока.

Рис. 1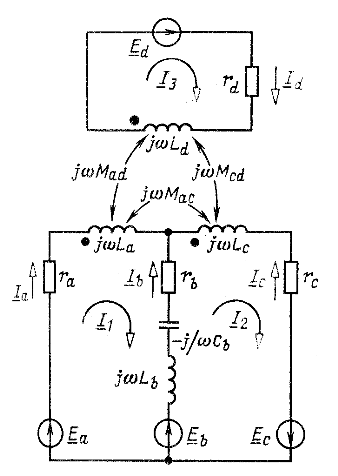

Приложение 3

Развязываниеиндуктивных связей

Расчет индуктивно связанных цепей осуществляют, как правило, по уравнениям Кирхгофа, так как применение других методов расчета имеет ряд особенностей. Однако если индуктивно связанные катушки имеют общий узел, бывает целесообразно преобразовать их в эквивалентную цепь, не содержащую индуктивных связей, после чего для анализа цепи можно применять все стандартные методы расчета. На рис. приведены две схемы индуктивно связанных катушек, имеющих общий узел, в котором сходятся либо однополярные выводы катушек, либо разнополярные, и соответствующие им эквивалентные схемы цепи без индуктивной связи (направление токов, т. е. характер включения катушек, может быть при этом произвольным).

Развязывание индуктивных связей осуществляется попарно ( раздельно для каждой пары катушек ) в соответствии с правилом для соединений катушек с разноименными (а) и одноименными (б) зажимами (Рис. 1)

а) б)

Рис. 1

Приложение 4

КОМПЛЕКСНЫЕ ЧИСЛА

Здесь идет повторение, а скорее первое знакомство студентов с комплексными числами в их традиционном представлении в курсе высшей математики, приобретении навыков над действиями комплексных чисел, решении комплексных уравнений, что способствует лучшему усвоению материала по комплексному (символическому) методу расчета и анализа линейных электрических цепей переменного тока.

Комплексные числа — расширение множества вещественных чисел, обычно обозначается C. Любое комплексное число может быть представлено как формальная сумма x+iy, где x и y — вещественные числа, i — мнимая единица, то есть одно из чисел, удовлетворяющих уравнению 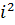=−1. Общепринятым произношением является компле́ксное число́, что позволяет различить математический смысл слова комплексный и бытовой.

Комплексные числа образуют алгебраически замкнутое поле и являются частным случаем гиперкомплексных чисел.

Итак. комплексным числом 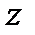называется арифметическое выражение вида

,

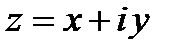(4.1)

где 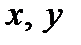- действительные числа, а 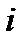- специальный символ, который называется мнимой единицей. Для мнимой единицы по определению считается, что .

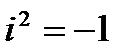(4.1) – алгебраическая форма комплексного числа, причем 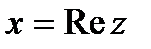называется действительной частью комплексного числа, а 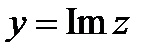- мнимой частью.

Число 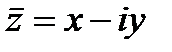называется комплексно сопряженным к числу .

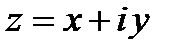Пусть даны два комплексных числа , .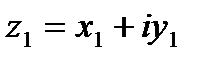

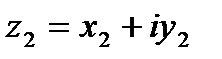1. Суммой 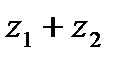комплексных чисел 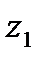и 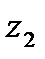называется комплексное число

.

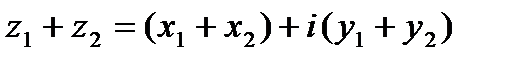2. Разностью 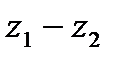комплексных чисел 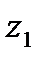и 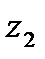называется комплексное число

.

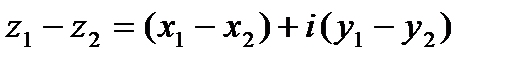3. Произведением 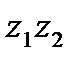комплексных чисел 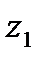и 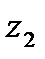называется комплексное число

.

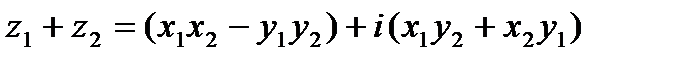4. Частным 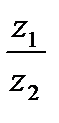от деления комплексного числа 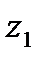на комплексное число 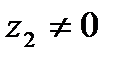называется комплексное число

.

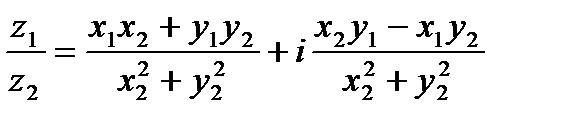Замечание 4.1. То есть операции над комплексными числами вводятся по обычным правилам арифметических операций над буквенными выражениями в алгебре.

Пример 4.1.Даны комплексные числа 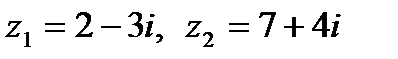. Найти

.

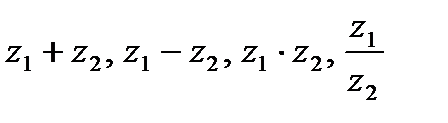Решение.1) .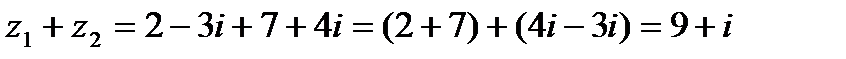

2) .

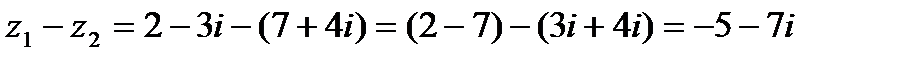3)

.

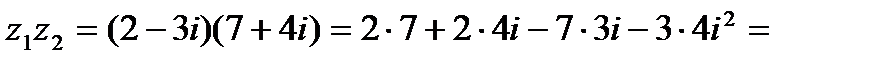
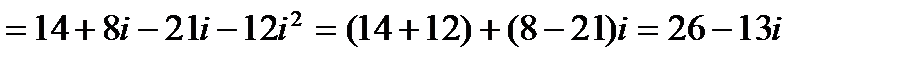4) Домножая числитель и знаменатель на комплексно сопряженное знаменателю число, получаем

.

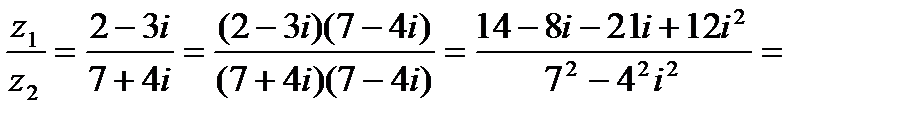
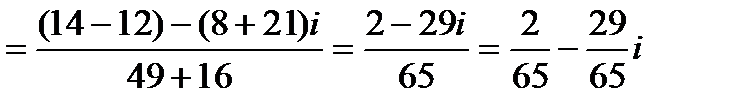Тригонометрическая формакомплексного числа:

,

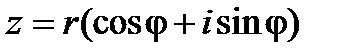где 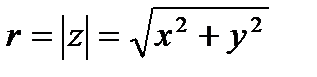- модуль комплексного числа, - аргумент комплексного числа. Угол 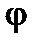определен неоднозначно, с точностью до слагаемого :

, .

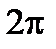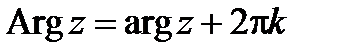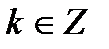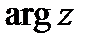- главное значение аргумента, определяемое условием

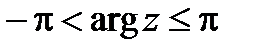, (или ).

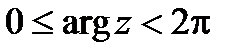Показательная форма комплексного числа:

.

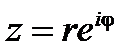Формула Муавра — формула, позволяющая возводить в степень комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

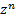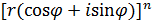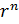= = (cos nφ + i sin nφ) =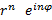

где 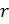— модуль, а φ — аргумент комплексного числа.

Корень 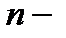й степени числа 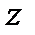имеет 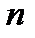различных значений, которые находятся по формуле

,

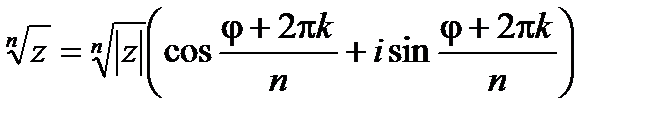(4.2)

где .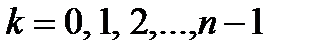

Точки, соответствующие значениям 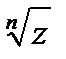, являются вершинами правильного 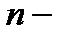угольника, вписанного в окружность радиуса 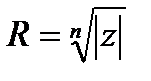с центром в начале координат.

Пример 4.2.Найти все значения корня .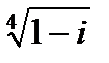

Решение.Представим комплексное число 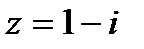в тригонометрической форме:

,

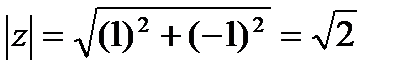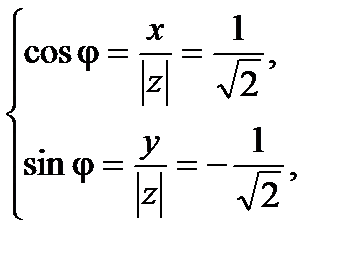, откуда .

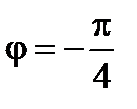Тогда 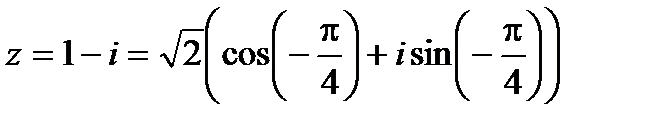. Следовательно, по формуле (4.2) 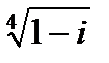имеет четыре значения:

, .

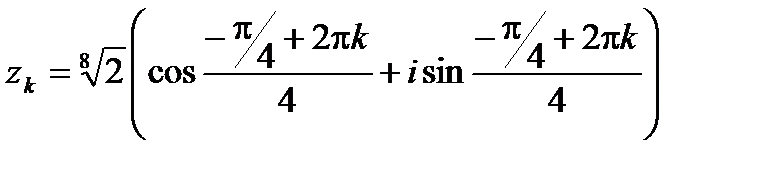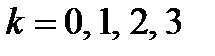Полагая 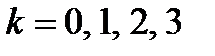, находим

, ,

, .

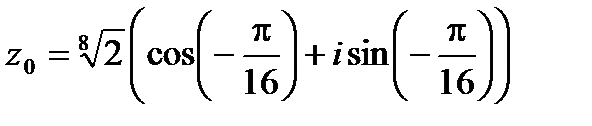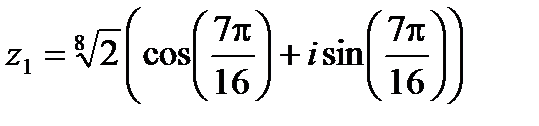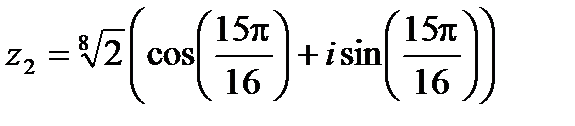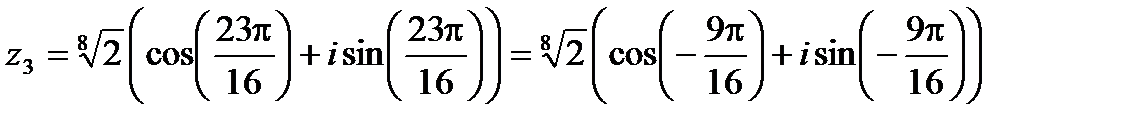Здесь мы преобразовывали значения аргумента к его главному значению.

Задача 1. Даны комплексные числа 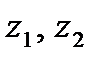. Найти .

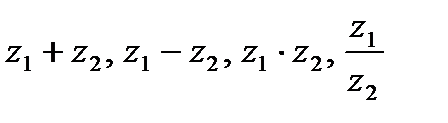1.1.	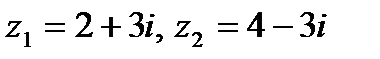1.2.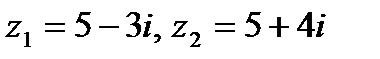
1.3.	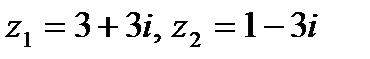1.4.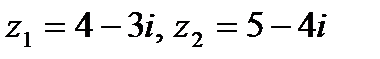
1.5.	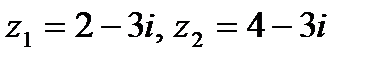1.6.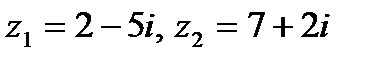
1.7.	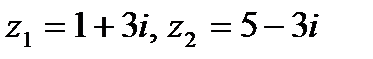1.8.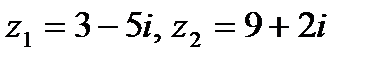
1.9.	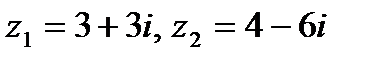1.10.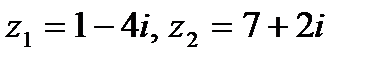
1.11.	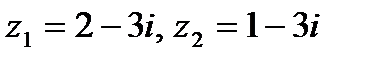1.12.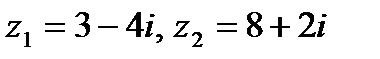
1.13.	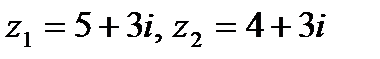1.14.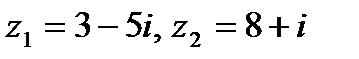
1.15.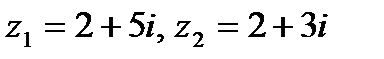	1.16.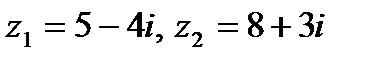
1.17.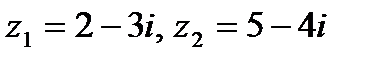	1.18.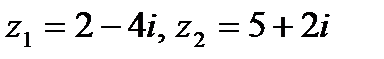
1.19.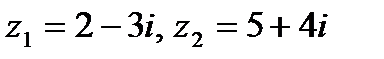	1.20.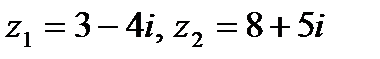
1.21.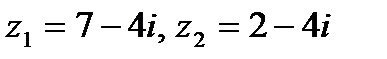	1.22.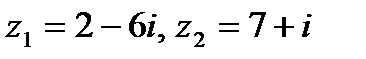
1.23.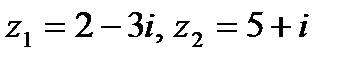	1.24.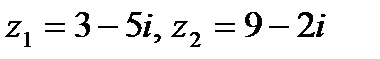
1.25.	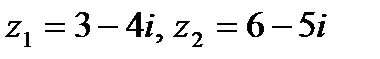1.26.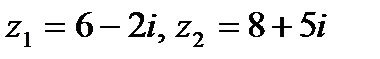
1.27.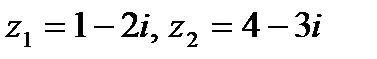	1.28.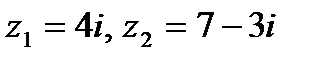
1.29.	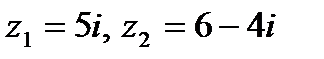1.30.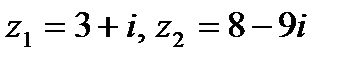

Задача 2. Найти все значения корня

2.1.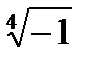	2.2.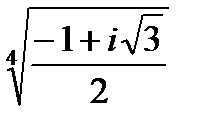
2.3.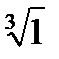	2.4.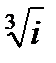
2.5.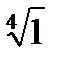	2.6.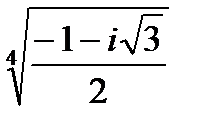
2.7.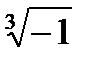	2.8.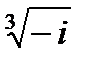
2.9.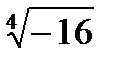	2.10.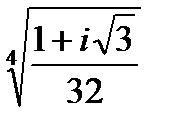
2.11.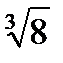	2.12.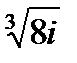
2.13.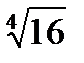	2.14.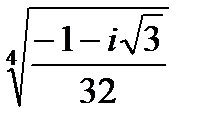
2.15.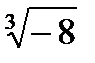	2.16.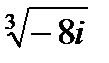
2.17.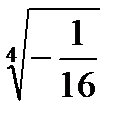	2.18.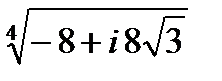
2.19.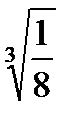	2.20.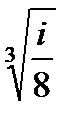
2.21.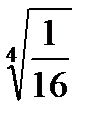	2.22.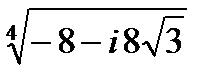
2.23.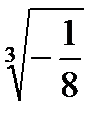	2.24.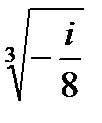
2.25.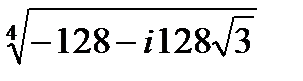	2.26.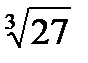
2.27.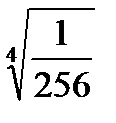	2.28.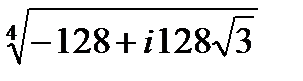
2.29.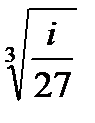	2.30.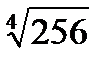

СПИСОК ЛИТЕРАТУРЫ

1. Письменный Д. Т. Конспект лекций по высшей математике: полный курс / Д. Т. Пись­менный – М.: Айрис-пресс, 2004.

2. Бугров Я.С. Высшая математика. Элементы линейной алгебры и аналитической геометрии / Я.С. Бугров. С.М. Никольский. – М.: Наука, 1984.

3. Высшая математика в упражнениях и задачах: учеб. пособие для вузов / П.Е. Данко [и др.] – 7изд., испр. – M.: ООО «Издательство Оникс»: ООО «Мир и Образование», 2008.

4. Кузнецов Л.А. Сборник заданий по высшей математике: типовые расчеты. / Л.А. Куз­нецов – СПб.: Издательство «Лань», 2007.

5. Марон И.А. Дифференциальное и интегральное исчисление в примерах и задачах. Функции одной переменной / И.А. Марон – М.: Наука, 1970.

6. Лебедева А.В. Высшая математика: комплекс учебно-методических материалов. Ч. 1 / А.В. Лебедева, С.В. Решетняк. Нижегород. гос. техн. ун-т. Нижний Новгород, 2006.

7. Кольчик И.В. Высшая математика: комплекс учебно-методических материалов. Ч. 2 / И.В, Кольчик. Нижегород. гос. техн. ун-т. Нижний Новгород, 2007.

8. Демирчян К.С., Нейман Л.Р. и др. Теоретические основы электротехники. Т.1. «Питер», 2003.

9. Теоретические основы электротехники. Основы теории линейных электрических цепей/ Под ред. П.А. Ионкина. М., 2008.

10. Шебес М.Р. Теория линейных электрических цепей а упражнениях и задачах. Издательство «Высшая школа». М., 1990.

11. Алтунин Б.Ю., Кралин А.А. и др. Теоретические основы электротехники. Часть 1, Учебное пособие. НГТУ., Н.Н., 2013.

12. Башев А.А., Кралин А.А. и др. Энергетическая электроника. Сборник задач. Часть 1, Учебное пособие. НГТУ., Н.Н., 2014.

13. Гольдфарб Н.И. Физика. Задачник, 10-11 классы. ДРОФА, М.,2010.

14. Фомина М.В. Решебник задач по физике. М., 2008.