Сведения из комбинаторики
Формулы комбинаторики часто используются для расчета конкретных вероятностей в задачах. Определим основные из них.
Ñ Перестановками из данных n элементов называются всевозможные соединения из этих элементов, различающихся только порядком.
· Сколько различных комбинаций, различающихся порядком следования элементов, можно образовать из трех предметов, например шаров, разного цвета: К – красного, Ж – желтого, З – зеленого?
- Таких комбинаций шесть: КЖЗ, КЗЖ, ЖКЗ, ЖЗК, ЗКЖ, ЗЖК. То есть количество перестановок из трех: 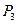 =6.
=6.
В общем случае, количество перестановок из n элементов: Pn =1´2´…´n = n!
В частности при n=3, P3 =1´2´3 = 3! = 6.
Ñ Сочетаниями из n элементов по m называются всевозможные соединения из m элементов, различающихся только составом элементов (независимо от порядка размещения).
· Сколько пар можно образовать из трех предметов (шаров) разного цвета (К, Ж, З)?
- Таких пар три (если не учитывать порядок следования): КЖ, КЗ, ЖЗ. То есть количество сочетаний из трех по два 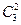 =3.
=3.
В общем случае, количество сочетаний из n по m дается формулой:
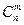 =
= 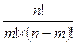
Ñ Размещениями из n различных элементов по m называются всевозможные соединения из m элементов, которые различаются либо составом, либо порядком своих элементов.
· Сколько всевозможных двузначных чисел можно образовать из цифр 1, 2, 3 (цифры не повторяются)?
- Таких чисел шесть: 12, 21, 13, 31, 23, 32. То есть количество размещений из трех по два 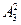 = 6.
= 6.
В общем случае, количество размещений из n по m дается формулой:
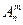 =
= 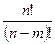
Задача: Из колоды в 36 карт наудачу извлекают две карты. Какова вероятность, что обе карты «пиковой масти»?
Решение: По определению вероятности р=т/п.
Здесь п= 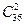 - сколько способов из 36 карт достать по 2 (порядок роли не играет), а
- сколько способов из 36 карт достать по 2 (порядок роли не играет), а
т= 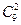 - сколько способов из 9 «пиковых» достать по 2. Тогда:
- сколько способов из 9 «пиковых» достать по 2. Тогда:
р=т/п= 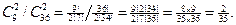
Дата добавления: 2016-06-05; просмотров: 1583;











