Свойства вероятности. Теоремы сложения и умножения
Ñ Суммой событий А и В называется событие С = А + В, состоящее в наступлении хотя бы одного из них.
Возможна также эквивалентная запись:
С = АÈВ (язык теории множеств),
С = А «или» В (логическая запись).
· Из колоды карт случайно достают одну. Если событие А={достается карта «червовой» масти}, В={карта «бубновой» масти}, то событие С=А+В будет, соответственно, С={карта «красной» масти}.
Теорема сложения вероятностей(случай несовместимых событий)
Вероятность суммы двух несовместимых событий А и В равна сумме их вероятностей: Р(А+В) = Р(А) + Р(В).
Следствие 1: Сумма вероятностей событий, образующих полную группу, равна 1.
· При подбрасывании игрального кубика, система событий:
E1 ={выпадение 1 очка}, E2 ={выпадение 2 очков}, …E6 ={выпадение 6 очков} -образует полную группу:
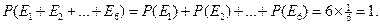
Следствие 2: Сумма вероятностей двух противоположных событий А и 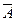 равна 1.
равна 1.
· Противоположные события – частный случай полной группы, состоящей из двух событий. Если, к примеру, вероятность попадания в мишень Р(А)=0,8, то вероятность промаха будет Р( 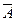 )=1-Р(А)=1-0,8=0,2.
)=1-Р(А)=1-0,8=0,2.
Ñ События А и В называются независимыми, если появление или непоявление одного из них не изменяет вероятность наступления другого.
· Предположим, что в урне 10 шаров, из них 6 белых и 4 черных. Опыт состоит в случайном доставании одного шара. Повторное доставание возможно в двух вариантах:
А) «С возвратом». Достали шар, посмотрели его цвет, вернули обратно. После перемешивания опыт повторили. Обозначим события:
А = {белый шар при первом доставании},
В = {белый шар при втором доставании}.
Очевидно, в данном случае, события А и В – независимы и Р(А)=Р(В)=0,6.
Б) «Без возврата». После доставания шар не возвращается обратно. В этом случае события зависимы и вводится понятие условной вероятности.
Если при первом доставании достали белый шар, то перед вторым доставанием остается 9 шаров, из них 5 белых и 4 черных. Можно сказать, что вероятность достать белый шар при втором доставании, при условии что при первом доставании был белый шар, равна 5/9, символически: 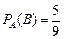 .
.
Ñ Произведением (или пересечением) событий А и В называется событие С, состоящее в совместном наступлении этих событий, т.е. в наступлении и события А и события В.
Записывается: С=А´В (алгебраическая запись), или
С=АÇВ (на языке теории множеств), или
С=А «и» В (логическая запись).
С использованием введенных обозначений, события А и В – независимы, если:
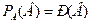 и
и 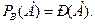
Дата добавления: 2016-06-05; просмотров: 1970;











