Теорема о движении центра масс
Общие теоремы динамики
Динамика системы материальных точек является важным разделом теоретической механики. Здесь в основном рассматриваются задачи о движении механических систем (систем материальных точек) с конечным числом степеней свободы – максимальным числом независимых параметров, определяющих положение системы. Главная задача динамики системы – изучение законов движения твердого тела и механических систем.
Наиболее простой подход к исследованию движения системы, состоящий из N материальных точек, сводиться к рассмотрению движений каждой отдельной точки системы. При этом должны быть определены все силы, действующие на каждую точку системы, в том числе и силы взаимодействия между точками.
Определяя ускорения каждой точки в соответствии со вторым законом Ньютона (1.2), получим для каждой точки три скалярных дифференциальных закона движения второго порядка, т.е. 3N дифференциальных закона движения для всей системы.
Для нахождения уравнений движения механической системы по заданным силам и начальным условиям для каждой точки системы, полученные дифференциальные законы нужно проинтегрировать. Эта задача трудна даже в случае двух материальных точек, которые движутся только под действием сил взаимодействия по закону всемирного притяжения (задача о двух телах), и исключительно трудна в случае трех взаимодействующих точек (задача о трех телах).
Поэтому необходимо отыскать такие методы решения задач, которые бы приводили к решаемым уравнениям и давали представление о движении механической системы. Общие теоремы динамики, являясь следствием дифференциальных законов движения, позволяют избежать сложности, возникающие при интегрировании и получать необходимые результаты.
Общие замечания
Точки механической системы будем нумеровать индексами i, j, k и т.д., которые пробегают все значения 1, 2, 3…N, где N – число точек системы. Физические величины, относящиеся к k-й точке, обозначаются таким же индексом, что и точка. Например, 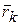 ,
, 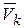 выражают соответственно радиус-вектор и скорость k-й точки.
выражают соответственно радиус-вектор и скорость k-й точки.
На каждую из точек системы действуют силы двоякого происхождения: во-первых, силы, источники которых лежат вне системы, называемые внешними силами и обозначаемые 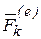 ; во-вторых, силы со стороны других точек данной системы, называемые внутренними силами и обозначаемые
; во-вторых, силы со стороны других точек данной системы, называемые внутренними силами и обозначаемые 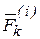 . Внутренние силы удовлетворяют третьему закону Ньютона. Рассмотрим простейшие свойства внутренних сил, действующих на всю механическую систему в любом ее состоянии.
. Внутренние силы удовлетворяют третьему закону Ньютона. Рассмотрим простейшие свойства внутренних сил, действующих на всю механическую систему в любом ее состоянии.
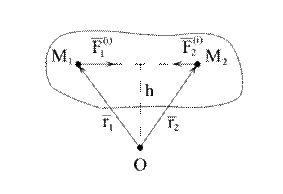 Рис. 3.1
Рис. 3.1
|
Первое свойство. Геометрическая сумма всех внутренних сил системы (главный вектор внутренних сил) равна нулю.
Действительно, если рассмотреть какие-либо две произвольные точки системы, например 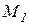 и
и 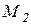 (рис. 3.1), то для них
(рис. 3.1), то для них 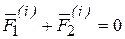 , т.к. силы действия и противодействия всегда равны по модулю, действуют вдоль одной линии действия в противоположном направлении, которое соединяет взаимодействующие точки. Главный вектор внутренних сил
, т.к. силы действия и противодействия всегда равны по модулю, действуют вдоль одной линии действия в противоположном направлении, которое соединяет взаимодействующие точки. Главный вектор внутренних сил 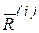 состоит из пар сил взаимодействующих точек, следовательно
состоит из пар сил взаимодействующих точек, следовательно
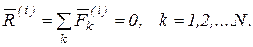 (3.1)
(3.1)
Второе свойство. Геометрическая сумма моментов всех внутренних сил относительно произвольной точки пространства равна нулю.
Рассмотрим систему моментов сил 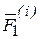 и
и 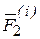 относительно точки О (рис.3.1). Из рис. 3.1. видно, что
относительно точки О (рис.3.1). Из рис. 3.1. видно, что
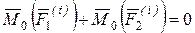 ,
,
т.к. обе силы имеют одинаковые плечи и противоположные направления векторных моментов. Главный момент внутренних сил 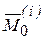 относительно точки О состоит из векторной суммы таких выражений и равен нулю. Следовательно,
относительно точки О состоит из векторной суммы таких выражений и равен нулю. Следовательно,
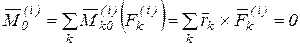 . k=1, 2,….N. (3.2)
. k=1, 2,….N. (3.2)
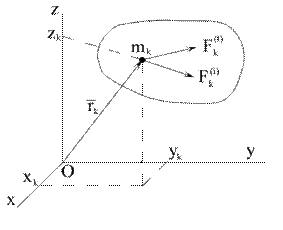 Рис. 3.2
Рис. 3.2
|
Пусть заданы внешние и внутренние силы, действующие на механическую систему, состоящую из N точек (рис. 3.2). Если к каждой точке системы приложить равнодействующую внешних сил  и
и
равнодействующую всех внутренних сил
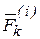 ,то для любой k-й точки системы можно составить дифференциальные уравнения движения. Всего таких уравнений будет N:
,то для любой k-й точки системы можно составить дифференциальные уравнения движения. Всего таких уравнений будет N:
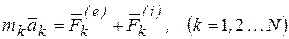 , (3.3)
, (3.3)
а в проекциях на неподвижные оси координат 3N:
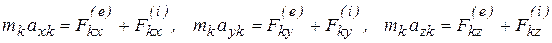 . (3.4)
. (3.4)
Векторные уравнения (3.3) или эквивалентные им скалярные уравнения (3.4) представляют дифференциальные законы движения материальных точек всей системы. Если все точки движутся параллельно одной плоскости или одной прямой, то число уравнений (3.4) в первом случае будет 2N, во втором N.
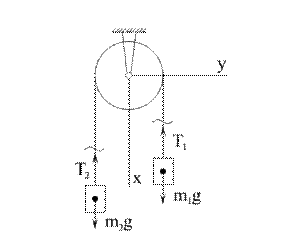 Рис. 3.3
Рис. 3.3
|
Пример 1. Два груза массой 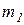 и
и 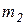 связаны между собой нерастяжимым тросом, перекинутым через блок (рис. 3.3). Пренебрегая силами трения, а также массой блока и троса, определить закон движения грузов и натяжения троса.
связаны между собой нерастяжимым тросом, перекинутым через блок (рис. 3.3). Пренебрегая силами трения, а также массой блока и троса, определить закон движения грузов и натяжения троса.
Решение. Система состоит из двух материальных тел (связанных нерастяжимым тросом), движущихся параллельно одной оси х. Запишем дифференциальные законы движения в проекциях на ось х для каждого тела.
Пусть правый груз опускается с ускорением 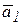 , тогда левый груз будет подниматься с ускорением
, тогда левый груз будет подниматься с ускорением 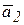 . Мысленно освобождаемся от связи (троса) и заменяем ее реакциями
. Мысленно освобождаемся от связи (троса) и заменяем ее реакциями 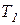 и
и 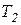 (рис. 3.3). Считая тела свободными, составим дифференциальные законы движения в проекции на ось х (имеется в виду, что натяжения нити являются внутренними силами, а вес грузов – внешними):
(рис. 3.3). Считая тела свободными, составим дифференциальные законы движения в проекции на ось х (имеется в виду, что натяжения нити являются внутренними силами, а вес грузов – внешними):
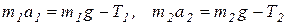 .
.
Поскольку 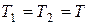 и
и 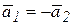 (тела связаны нерастяжимым тросом), получаем
(тела связаны нерастяжимым тросом), получаем

Решая эти уравнения относительно ускорения 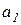 и натяжения троса Т, получим
и натяжения троса Т, получим
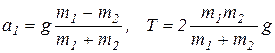 .
.
Отметим, что натяжение троса при 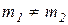 не равно силе тяжести соответствующего груза.
не равно силе тяжести соответствующего груза.
Теорема о движении центра масс
Известно, что твердое тело и механическая система в плоскости может двигаться достаточно сложно. К первой теореме о движении тела и механической системы можно прийти следующим образом: бросить к.-л. предмет, состоящий из множества скрепленных между собой твердых тел. Ясно, что он полетит по параболе. Это выявилось при изучении движения точки. Однако теперь объект не точка. Он поворачивается, покачивается в процессе полета вокруг некого эффективного центра, который движется по параболе. Первая теорема о движении сложных предметов говорит о том, что некий эффективный центр есть центр масс движущегося предмета. Центр масс не обязательно находится в самом теле, он может лежать и где-то вне его.
Теорема. Центр масс механической системы движется как материальная точка массой равной массе всей системы, к которой приложены все внешние силы, действующие на систему.
Для доказательства теоремы перепишем дифференциальные законы движения (3.3) в следующем виде:
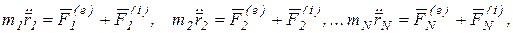 (3.5)
(3.5)
где N – число точек системы.
Сложим почленно уравнения между собой:
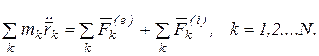 (а)
(а)
Положение центра масс механической системы относительно выбранной системы координат определяется формулой (2.1): 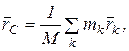 где М – масса системы. Тогда левая часть равенства (а) запишется
где М – масса системы. Тогда левая часть равенства (а) запишется
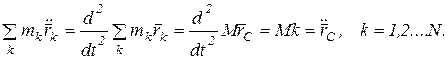 (б)
(б)
Первая сумма, стоящая в правой части равенства (а), равна главному вектору 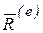 внешних сил, а последняя по свойству внутренних сил равна нулю. Тогда равенство (а), с учетом (б) перепишется
внешних сил, а последняя по свойству внутренних сил равна нулю. Тогда равенство (а), с учетом (б) перепишется
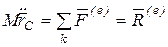 , (3.6)
, (3.6)
т.е. произведение массы системы на ускорение центра ее массы равно геометрической сумме всех действующих на систему внешних сил.
Из уравнения (3.6) следует, что внутренние силы непосредственно не влияют на движение центра масс. Однако в ряде случаев являются причиной появления внешних сил, приложенных к системе. Так, внутренние силы, приводящие во вращение ведущие колеса автомобиля, вызывают действие на него внешней силы сцепления, приложенной к ободу колеса.
Пример 2. Механизм, расположенный в вертикальной плоскости, установлен на горизонтальной гладкой плоскости и прикреплен к ней жестко закрепленными с поверхностью брусками К и L (рис. 3.4).
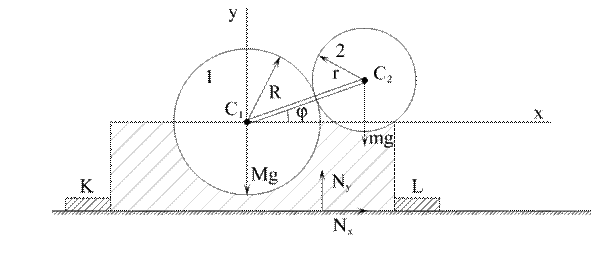
Рис.3.4
Диск 1 радиусом R неподвижен. Диск 2 массой m и радиусом r скреплен с кривошипом 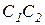 , длиной R+r в точке С2. Кривошип вращается с постоянной
, длиной R+r в точке С2. Кривошип вращается с постоянной
угловой скоростью 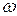 . В начальный момент кривошип занимал правое горизонтальное положение. Пренебрегая массой кривошипа, определить наибольшее горизонтальное и вертикальное усилия, действующие на бруски, если общая масса станины и колеса 1 равна М. Также рассмотреть поведение механизма при отсутствии брусков.
. В начальный момент кривошип занимал правое горизонтальное положение. Пренебрегая массой кривошипа, определить наибольшее горизонтальное и вертикальное усилия, действующие на бруски, если общая масса станины и колеса 1 равна М. Также рассмотреть поведение механизма при отсутствии брусков.
Решение. Система состоит из двух масс (N=2): неподвижного диска 1 со станиной и подвижного диска 2. Направим ось у через центр тяжести неподвижного диска по вертикали вверх, ось х – вдоль горизонтальной плоскости.
Запишем теорему о движении центра масс (3.6) в координатной форме
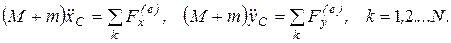 (б)
(б)
Внешними силами этой системы являются: вес станины и неподвижного диска – Mg, вес подвижного диска – mg, 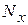 - суммарная горизонтальная реакция болтов,
- суммарная горизонтальная реакция болтов, 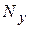 - нормальная суммарная реакция плоскости. Следовательно,
- нормальная суммарная реакция плоскости. Следовательно,
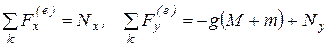 . (в)
. (в)
Тогда законы движения (б) перепишутся
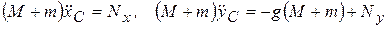 .
.
Вычислим координаты центра масс механической системы:
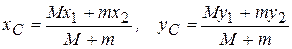 ; (г)
; (г)
как видно из рис. 3.4, 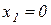 ,
, 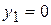 ,
, 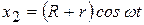 (угол поворота кривошипа
(угол поворота кривошипа 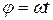 ),
), 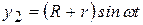 . Подставляя эти выражения в (г) и вычисляя вторые производные по времени t от
. Подставляя эти выражения в (г) и вычисляя вторые производные по времени t от  ,
, 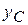 , получим, что
, получим, что
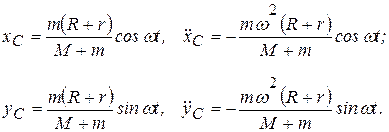 (д)
(д)
Подставляя (в) и (д) в (б), находим
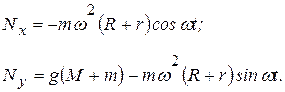
Горизонтальное давление, действующее на бруски, имеет наибольшее и наименьшее значения, когда cos 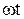 =
= 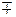 1 соответственно, т.е
1 соответственно, т.е
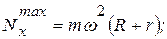
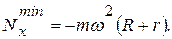
Давление механизма на горизонтальную плоскость имеет наибольшее и наименьшее значения, когда sin 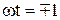 соответственно, т.е.
соответственно, т.е.
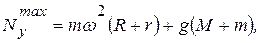
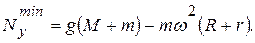
Фактически решена первая задача динамики: по известным уравнениям движения центра масс системы (д) восстанавливаются силы, участвующие в движении.
В условиях отсутствия брусков K и L (рис. 3.4), механизм может начать подпрыгивать над горизонтальной плоскостью. Это будет иметь место, когда 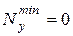 , т.е. когда
, т.е. когда 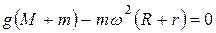 , отсюда следует, что угловая скорость
, отсюда следует, что угловая скорость 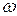 вращения кривошипа, при которой происходит подпрыгивание механизма, должна удовлетворять равенству
вращения кривошипа, при которой происходит подпрыгивание механизма, должна удовлетворять равенству
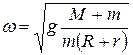 .
.
Дата добавления: 2019-12-09; просмотров: 521;











