Разработка тестовых шкал
Тестовые шкалы разрабатываются для того, чтобы оценить индивидуальный результат тестирования путем сопоставления его с тестовыми нормами, полученными на выборке стандартизации. Выборка стандартизации специально формируется для разработки тестовой шкалы – она должна быть репрезентативна генеральной совокупности, для которой планируется применять данный тест. Впоследствии при тестировании предполагается, что и тестируемый, и выборка стандартизации принадлежат одной и той же генеральной совокупности.
Исходным принципом при разработке тестовой шкалы является предположение о том, что измеряемое свойство распределено в генеральной совокупности в соответствии с нормальным законом. Соответственно, измерение в тестовой шкале данного свойства на выборке стандартизации также должно обеспечивать нормальное распределение. Если это так, то тестовая шкала является метрической – точнее, равных интервалов. Если это не так, то свойство удалось отразить в лучшем случае – в шкале порядка. Естественно, что большинство стандартных тестовых шкал являются метрическими, что позволяет более детально интерпретировать результаты тестирования – с учетом свойств нормального распределения – и корректно применять любые методы статистического анализа. Таким образом, основная проблема стандартизации теста заключается в разработке такой шкалы, в которой распределение тестовых показателей на выборке стандартизации соответствовало бы нормальному распределению.
Исходные тестовые оценки – это количество ответов на те или иные вопросы теста, время или количество решенных задач и т. д. Они еще называются первичными, или «сырыми» оценками. Итогом стандартизации являются тестовые нормы – таблица пересчета «сырых» оценок в стандартные тестовые шкалы.
Существует множество стандартных тестовых шкал, основное назначение которых – представление индивидуальных результатов тестирования в удобном для интерпретации виде. Некоторые из этих шкал представлены на рисунке 6.5. Общим для них является соответствие нормальному распределению, а различаются они только двумя показателями: средним значением и масштабом (стандартным отклонением – σ), определяющим дробность шкалы.
Общая последовательность стандартизации (разработки тестовых норм – таблицы пересчета «сырых» оценок в стандартные тестовые) состоит в следующем:
1) определяется генеральная совокупность, для которой разрабатывается методика и формируется репрезентативная выборка стандартизации;
2) по результатам применения первичного варианта теста строится распределение «сырых» оценок;
3) проверяют соответствие полученного распределения нормальному закону;
4) если распределение «сырых» оценок соответствует нормальному, производится линейная стандартизация;
5) если распределение «сырых» оценок не соответствует нормальному, то возможны два варианта:
• перед линейной стандартизацией производят эмпирическую нормализацию;
• проводят нелинейную нормализацию.
Проверка распределения «сырых» оценок на соответствие нормальному закону производится при помощи специальных критериев, которые мы рассмотрим далее в этой главе.
Линейная стандартизация заключается в том, что определяются границы интервалов «сырых» оценок, соответствующие стандартным тестовым показателям. Эти границы вычисляются путем прибавления к среднему «сырых» оценок (или вычитания из него) долей стандартных отклонений, соответствующих тестовой шкале. Пример, приведенный ниже, демонстрирует процедуру линейной стандартизации.
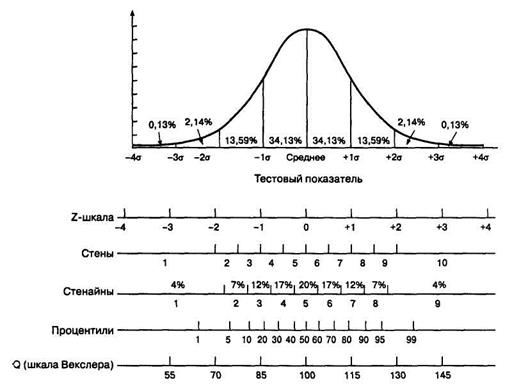
Рис. 6.5. Нормальная кривая и тестовые шкалы
Пример.Предположим, получено распределение «сырых» оценок, соответствующее нормальному, со средним Мх = 22 и стандартным отклонением σх = 6. В качестве стандартной тестовой шкалы выбрана 10-балльная шкала стенов, предложенная Р. Кеттелом (Mst = 5,5; σst = 2). Результатом линейной стандартизации должна являться таблица пересчета из шкалы «сырых» оценок в шкалу стенов. Для этого каждому стандартному значению ставится в соответствие интервал «сырых» оценок. Границы интервалов определяются следующим образом. Среднее «сырых» оценок должно делить шкалу стенов ровно пополам (1 – 5 – ниже среднего, 6 – 10 – выше среднего). Следовательно, среднее «сырых» оценок Мх=22 – это граница стенов 5 и 6. Следующая граница справа – отделяющая стены 6 и 7 – отстоит от среднего на σst/2. Этой границе должна соответствовать граница «сырых» оценок Мх + σst/2 = 22 + 3 = 25. Так же определяются границы всех оставшихся интервалов, а границы крайних интервалов остаются открытыми. Результатом являются тестовые нормы – таблица пересчета «сырых» баллов в стандартные тестовые оценки (табл. 6.1).
Обратите внимание, что левая граница каждого диапазона «сырых» оценок исключает границу интервалов, а правая – включает ее. Можно было бы сделать и наоборот, но главное, чтобы границы соседних диапазонов не совпадали во избежание недоразумений при попадании индивидуального значения на границу интервалов.
Таблица 6.1
Тестовые нормы – таблица пересчета «сырых» баллов в стены
| стены | ||||||||||
| «сырые» баллы | <11 | 11-13 | 14-16 | 17-19 | 20-22 | 23-25 | 26-28 | 29-31 | 32-34 | >34 |
Пользуясь этой таблицей тестовых норм, индивидуальный результат («сырой» балл) переводят в шкалу стенов, что позволяет интерпретировать выраженность измеряемого свойства.
В общем случае границы интервалов определяются по формуле z-преобразования:
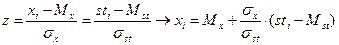 ,
,
где xi – искомая граница интервала «сырых» оценок, sti – граница интервала «стандартной» тестовой шкалы, Мх, σх, Mst, σst – средние и стандартные отклонения «сырых» оценок (х) и стандартной шкалы (st).
Эмпирическая нормализация применяется, когда распределение «сырых» баллов отличается от нормального. Она заключается в изменении содержания тестовых заданий. Например, если «сырая» оценка – это количество задач, решенных испытуемыми за отведенное время, и получено распределение с правосторонней асимметрией, то это значит, что слишком большая доля испытуемых решает больше половины заданий. В этом случае необходимо либо добавить более трудные задания, либо сократить время решения.
Нелинейная нормализация применяется, если эмпирическая нормализация невозможна или нежелательна, например, с точки зрения затрат времени и ресурсов. В этом случае перевод «сырых» оценок в стандартные производится через нахождение процентильных границ групп в исходном распределении, соответствующих процентильным границам групп в нормальном распределении стандартной шкалы. Каждому интервалу стандартной шкалы ставится в соответствие такой интервал шкалы «сырых» оценок, который содержит ту же процентную долю выборки стандартизации. Величины долей определяются по площади под единичной нормальной кривой, заключенной между соответствующими данному интервалу стандартной шкалы z-оценками.
Например, для того чтобы определить, какой «сырой» балл должен соответствовать нижней границе стена 10, необходимо сначала выяснить, какому z-значению соответствует эта граница (z = 2). Затем по таблице нормального распределения (приложение 1) надо определить, какая доля площади под нормальной кривой находится правее этого значения (0,023). После этого определяется, какое значение отсекает 2,3% наибольших значений «сырых» баллов выборки стандартизации. Найденное значение и будет соответствовать границе 9 и 10 стена.
Пример.Рассмотрим пример нелинейной нормализации. Допустим, разрабатываемый тест предполагает решение 20 заданий. Объем выборки стандартизации N = 200 человек. Сначала строится таблица распределения частот «сырых» оценок (табл. 6.2).
Таблица 6.2
Таблица распределения частот «сырых» оценок
| оценка | |||||||||||||||||||
| частота |
Исходное распределение заметно отличается от нормального – оно имеет правостороннюю асимметрию (рис. 6). В качестве стандартной выберем шкалу стенайнов, для каждой градации которой известны процентные доли (рис. 6.5). Исходя из этих процентных долей и таблицы распределения «сырых» оценок строится таблица тестовых норм (табл. 6.3). Сначала отбираются 4% испытуемых, решивших наименьшее количество заданий. У нас 8 испытуемых (4%) решили менее 4 заданий. Это число заданий будет соответствовать 1-му стенайну. Второму стенайну будет соответствовать результат следующих 7% (14) испытуемых: от 4 до 6 заданий, и т. д. Итог нелинейной стандартизации – таблица перевода «сырых» оценок в шкальные, стенайны (табл. 6.3).
Таблица 6.3
Дата добавления: 2021-11-16; просмотров: 653;











