Проверка нормальности распределения

Для проверки нормальности используются различные процедуры, позволяющие выяснить, отличается ли от нормального выборочное распределение измеренной переменной. Необходимость такого сопоставления возникает, когда мы сомневаемся в том, в какой шкале представлен признак – в порядковой или метрической. А сомнения такие возникают очень часто, так как заранее нам, как правило, не известно, в какой шкале удастся измерить изучаемое свойство (исключая, конечно, случаи явно номинативного измерения).

Важность определения того, в какой шкале измерен признак, трудно переоценить, по крайней мере, по двум причинам. От этого зависит, во-первых, полнота учета исходной эмпирической информации (в частности, об индивидуальных различиях), во-вторых, доступность многих методов анализа данных. Если исследователь принимает решение об измерении в порядковой шкале, то неизбежное последующее ранжирование ведет к потере части исходной информации о различиях между испытуемыми, изучаемыми группами, о взаимосвязях между признаками и т. д. Кроме того, метрические данные позволяют использовать значительно более широкий набор методов анализа и, как следствие, сделать выводы исследования более глубокими и содержательными.

Наиболее весомым аргументом в пользу того, что признак измерен в метрической шкале, является соответствие выборочного распределения нормальному. Это является следствием закона нормального распределения. Если выборочное распределение не отличается от нормального, то это значит, что измеряемое свойство удалось отразить в метрической шкале (обычно – интервальной).

Существует множество различных способов проверки нормальности, из которых мы кратко опишем лишь некоторые.

Графический способ. Строят либо квантильные графики, либо графики накопленных частот. Квантильные графики строятся следующим образом. Сначала определяются эмпирические значения изучаемого признака, соответствующие 5, 10,..., 95-процентилю. Затем по таблице нормального распределения для каждого из этих процентилей определяются z-значения (теоретические). Два полученных ряда чисел задают координаты точек на графике: эмпирические значения признака откладываются на оси абсцисс, а соответствующие им теоретические значения – на оси ординат. Для нормального распределения все точки будут лежать на одной прямой или рядом с ней. Чем больше расстояние от точек до прямой линии, тем меньше распределение соответствует нормальному. Графики накопленных частот строятся подобным образом. На оси абсцисс через равные интервалы откладываются значения накопленных относительных частот, например, 0,05; 0,1;...; 0,95. Далее определяются эмпирические значения изучаемого признака, соответствующие каждому значению накопленной частоты, которые пересчитываются в z-значения. По таблице нормального распределения определяются теоретические накопленные частоты (площадь под кривой) для каждого из вычисленных z-значений, которые откладываются на оси ординат. Если распределение соответствует нормальному, полученные на графике точки лежат на одной прямой.

Критерии асимметрии и эксцесса. Эти критерии определяют допустимую степень отклонения эмпирических значений асимметрии и эксцесса от нулевых значений, соответствующих нормальному распределению. Допустимая степень отклонения – та, которая позволяет считать, что эти статистики существенно не отличаются от нормальных параметров. Величина допустимых отклонений определяется так называемыми стандартными ошибками асимметрии и эксцесса. Для формулы асимметрии

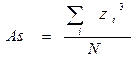
стандартная ошибка определяются по формуле:

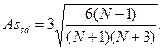
Для формулы эксцесса

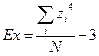
стандартная ошибка эксцесса:

,

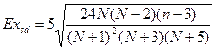где N – объем выборки.

Выборочные значения асимметрии и эксцесса значительно отличаются от нуля, если не превышают значения своих стандартных ошибок. Это можно считать признаком соответствия выборочного распределения нормальному закону. Следует отметить, что компьютерные программы вычисляют показатели асимметрии, эксцесса и соответствующие им стандартные ошибки по другим, более сложным формулам.

Статистический критерий нормальности Колмогорова-Смирнова считается наиболее состоятельным для определения степени соответствия эмпирического распределения нормальному. Он позволяет оценить вероятность того, что данная выборка принадлежит генеральной совокупности с нормальным распределением. Если эта вероятность р ≤ 0,05, то данное эмпирическое распределение существенно отличается от нормального, а если р > 0,05, то делают вывод о приблизительном соответствии данного эмпирического распределения нормальному.

Причины отклонения от нормальности. Общей причиной отклонения формы выборочного распределения признака от нормального вида чаще всего является особенность процедуры измерения: используемая шкала может обладать неравномерной чувствительностью к измеряемому свойству в разных частях диапазона его изменчивости.

Пример. Предположим, выраженность некоторой способности определяется количеством выполненных заданий за отведенное время. Если задания простые или время слишком велико, то данная измерительная процедура будет обладать достаточной чувствительностью лишь в отношении части испытуемых, для которых эти задания достаточно трудны. И слишком большая доля испытуемых будет решать все или почти все задания. В итоге мы получим распределение с выраженной правосторонней асимметрией. Можно, конечно, впоследствии повысить качество измерения путем эмпирической нормализации, добавив более сложные задания или сократив время выполнения данного набора заданий. Если же мы чрезмерно усложним измерительную процедуру, то возникнет обратная ситуация, когда большая часть тестуемых будет решать малое количество заданий и эмпирическое распределение приобретет левостороннюю асимметрию.

Таким образом, такие отклонения от нормального вида, как право- или левосторонняя асимметрия или слишком большой эксцесс (больше 0), связаны с относительно низкой чувствительностью измерительной процедуры в области моды (вершины графика распределения частот).

Последствия отклонения от нормальности. Следует отметить, что задача получения эмпирического распределения, строго соответствующего нормаль­ному закону, нечасто встречается в практике исследования. Обычно такие случаи ограничиваются разработкой новой измерительной процедуры или тестовой шкалы, когда применяется эмпирическая или нелинейная нормализация для «исправления» эмпирического распределения. В большинстве случаев соответствие или несоответствие нормальности является тем свойством измеренного признака, который исследователь должен учитывать при выборе статистических процедур анализа данных.

В общем случае при значительном отклонении эмпирического распределения от нормального следует отказаться от предположения о том, что признак измерен в метрической шкале. Но остается открытым вопрос о том, какова мера существенности этого отклонения? Кроме того, разные методы анализа данных обладают различной чувствительностью к отклонениям от нормальности. Обычно при обосновании перспективности этой проблемы приводят принцип Р. Фишера, одного из «отцов-основателей» современной статистики: «Отклонения от нормального вида, если только они не слишком заметны, можно обнаружить лишь для больших выборок; сами по себе они вносят малое отличие в статистические критерии и другие вопросы». К примеру, при малых, но обычных для психологических исследований выборках (до 50 человек) критерий Колмогорова-Смирнова недостаточно чувствителен при определении даже весьма заметных «на глаз» отклонений от нормальности. В то же время некоторые процедуры анализа метрических данных вполне допускают отклонения от нормального распределения (одни – в большей степени, другие – в меньшей). В дальнейшем при изложении материала мы при необходимости будем оговаривать меру жесткости требования нормальности.