Квантили распределения
Помимо мер центральной тенденции в психологии широко используются меры положения, которые называются квантилями распределения. Квантиль − это точка на числовой оси измеренного признака, которая делит всю совокупность упорядоченных измерений на две группы с известным соотношением их численности. С одним из квантилей мы уже знакомы − это медиана. Это значение признака, которое делит всю совокупность измерений на две группы с равной численностью. Кроме медианы часто используются процентили и квартили.
Процентили − это 99 точек − значений признака (Р1, ..., Р99), которые делят упорядоченное (по возрастанию) множество наблюдений на 100 частей, равных по численности. Определение конкретного значения процентиля аналогично определению медианы. Например, при определении 10-го процентиля, Р10, сначала все значения признака упорядочиваются по возрастанию. Затем отсчитывается 10% испытуемых, имеющих наименьшую выраженность признака. Р10 будет соответствовать тому значению признака, который отделяет эти 10% испытуемых от остальных 90%.
Квартили − это 3 точки − значения признака (P25, Р50, Р75), которые делят упорядоченное (по возрастанию) множество наблюдений на 4 равные по численности части. Первый квартиль соответствует 25-му процентилю, второй − 50-му процентилю или медиане, третий квартиль соответствует 75-му процентилю.
Процентили и квартили используются для определения частоты встречаемости тех или иных значений (или интервалов) измеренного признака или для выделения подгрупп и отдельных испытуемых, наиболее типичных или нетипичных для данного множества наблюдений.
Меры изменчивости
Меры центральной тенденции отражают уровень выраженности измеренного признака. Однако не менее важной характеристикой является выраженность индивидуальных различий испытуемых по измеренному признаку. Меры изменчивости применяются в психологии для численного выражения величины межиндивидуальной вариации признака.
Наиболее простой и очевидной мерой изменчивости является размах, указывающий на диапазон изменчивости значений. Размах − это просто разность максимального и минимального значений:
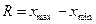 .
.
Ясно, что это очень неустойчивая мера изменчивости, на которую влияют любые возможные «выбросы». Более устойчивыми являются разновидности размаха: размах от 10 до 90-го процентиля (P90 – P10) или междуквартильный размах (Р75 – Р25). Последние две меры изменчивости находят свое применение для описания вариации в порядковых данных. А для метрических данных используется дисперсия − величина, название которой в науке является синонимом изменчивости.
Дисперсия − мера изменчивости для метрических данных, пропорциональная сумме квадратов отклонений измеренных значений от их арифметического среднего:
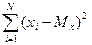 .
.
Чем больше изменчивость в данных, тем больше отклонения значений от среднего, тем больше величина дисперсии. Величина дисперсии получается при усреднении всех квадратов отклонений:
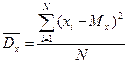 .
.
Следует отличать теоретическую (генеральную) дисперсию − меру изменчивости бесконечного числа измерений (в генеральной совокупности, популяции в целом) и эмпирическую, или выборочную, дисперсию – для реально измеренного множества значений признака. Выборочное значение в статистике используется для оценки дисперсии в генеральной совокупности. Выше указана формула для генеральной (теоретической) дисперсии ( 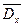 ), которая, понятно, не вычисляется. Для вычислений используется формула выборочной (эмпирической) дисперсии (Dx), отличающаяся знаменателем:
), которая, понятно, не вычисляется. Для вычислений используется формула выборочной (эмпирической) дисперсии (Dx), отличающаяся знаменателем:
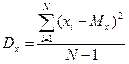 .
.
Пример.Вычислим дисперсию признака Х для выборки N = 6:
| № | xi | (xi – Mx) | (xi – Mx)2 |
| 4 – 3 | |||
| 2 – 3 | |||
| 4 – 3 | |||
| 1 – 3 | |||
| 5 – 3 | |||
| 2 – 3 | |||
| ∑ |
Мх = 18 : 6 = 3; Dx= 12 : (6 – 1) = 2,4.
Стандартное отклонение 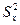 или среднеквадратическое отклонение σ (сигма) − положительное значение квадратного корня из дисперсии:
или среднеквадратическое отклонение σ (сигма) − положительное значение квадратного корня из дисперсии:
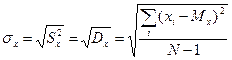 .
.
На практике чаще используется именно стандартное отклонение, а не дисперсия. Это связано с тем, что сигма выражает изменчивость в исходных единицах измерения признака, а дисперсия − в квадратах исходных единиц.
Свойства дисперсии.
1. Если значения измеренного признака не отличаются друг от друга (равны между собой) − дисперсия равна нулю. Это соответствует отсутствию изменчивости в данных.
2. Прибавление одного и того же числа к каждому значению переменной не меняет дисперсию:
Dx+c = Dx, так как ∑[(xi + c) – (Mx + c)]2 = ∑(xi – Mx)2.
Прибавление константы к каждому значению переменной сдвигает график распределения этой переменной на эту константу (меняется среднее), но изменчивость (дисперсия) при этом остается неизменной.
3. Умножение каждого значения переменной на константу с изменяет дисперсию в с2 раз:
Dx∙c = Dx∙c2, так как ∑[(хi∙с) − (Mx∙с)]2 = c2∙∑(xi – Мх)2.
При объединении двух выборок с одинаковой дисперсией, но с разными средними значениями дисперсия увеличивается.
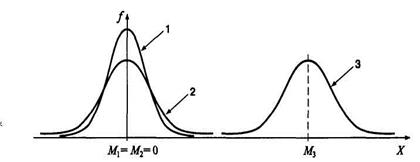
Рис. 5.1. Графики распределения частот: с разной дисперсией
(D1 < D2), одинаковой дисперсией (D2 = D3) и разными средними арифметическими (M2 < M3)
Пример.Если одна группа содержит значения: 1, 1, 1, 1, 1, а другая группа − значения 3, 3, 3, 3, 3, то дисперсии этих групп одинаковы и равны 0. Если же объединить эти две группы, то дисперсия будет равна не 0, а 1.
Вообще говоря, справедливо утверждение: при объединении двух групп к внутригрупповой дисперсии каждой группы добавляется дисперсия, обусловленная различием между группами (их средними). И чем больше различие между средними значениями, тем больше увеличивается дисперсия объединенных групп.
Стандартизацияили z-преобразование данных − это перевод измерений в стандартную Z-шкалу со средним Мz = 0 и Dz (или σz) = 1. Сначала для переменной, измеренной на выборке, вычисляют среднее Мх стандартное отклонение σх. Затем все значения переменной хi, пересчитываются по формуле:
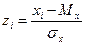 . (5.1)
. (5.1)
В результате преобразованные значения (z-значения) непосредственно выражаются в единицах стандартного отклонения от среднего. Если для одной выборки несколько признаков переведены в z-значения, появляется возможность сравнения уровня выраженности разных признаков у того или иного испытуемого. Для того чтобы избавиться от неизбежных отрицательных и дробных значений, можно перейти к любой другой известной шкале: IQ (среднее 100, сигма 15); Т-оценок (среднее 50, сигма 10); 10-балльной − стенов (среднее 5, 5, сигма 2) и др. Перевод в новую шкалу осуществляется путем умножения каждого z-значения на заданную сигму и прибавления среднего:
Si = σs∙zi + Ms.
Асимметрия − степень отклонения графика распределения частот от симметричного вида относительно среднего значения. Если исходные данные переведены в z-значения, показатель асимметрии вычисляется по формуле:

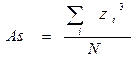 .
.
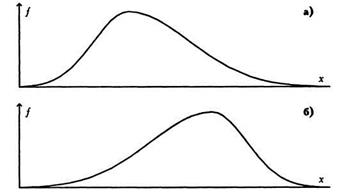
Рис. 5.2. Асимметрия распределений:
а) левосторонняя, положительная;
б) правосторонняя, отрицательная
Для симметричного распределения асимметрия равна 0. Если чаще встречаются значения меньше среднего, то говорят о левосторонней, или положительной асимметрии (As > 0). Если же чаще встречаются значения больше среднего, то асимметрия − правосторонняя, или отрицательная (As < 0). Чем больше отклонение от нуля, тем больше асимметрия.
Эксцесс − мера плосковершинности или остроконечности графика распределения измеренного признака. Если исходные данные переведены в z-значения, показатель эксцесса определяется формулой:
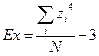 .
.
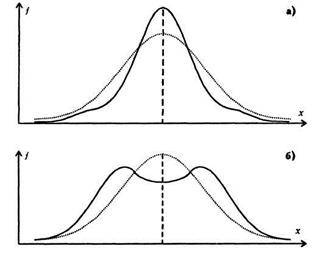
Рис. 5.3. Эксцесс: а) положительный; б) отрицательный
Островершинное распределение характеризуется положительным эксцессом (Ех > 0), а плосковершинное − отрицательным (-3 < Ех < 0). «Средневершинное» (нормальное) распределение имеет нулевой эксцесс (Ех = 0).
Дата добавления: 2021-11-16; просмотров: 725;











