Линейная парная корреляция. Коэффициент корреляции

Если обе линии регрессии 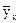=f(x) и 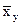= j(у) являются прямыми линиями, то корреляция называется линейной.

Эмпирическое (выборочное) уравнение прямой линии регрессии У на X имеет вид:

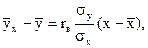(11)

где 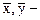выборочные средние признаков Х и У, 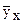- условная средняя (среднее арифметическое наблюдавшихся значений У, соответствующих конкретному значению X=х; s_х и s_у - выборочные средние квадратические отклонения; r_в =r_ху - выборочный коэффициент корреляции, служащий для оценки степени линейной корреляционной связи:
(-1 £ r_в £ 1). Чем ближе |r_в| к единице, тем это связь сильнее, и наоборот, чем ближе |r_в| к нулю, тем связь слабее. Равенство коэффициента корреляции нулю означает отсутствие линейной корреляционной зависимости между СВ Хм У, но не отсутствие корреляции вообще, которая может оказаться нелинейной. Если |r_в|, =1 , то между X и У имеется линейная функциональная зависимость - каждому значению х соответствует только одно значение у.

Для нахождения 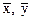, s_х, s_у и r_в используются формулы:

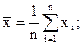
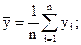
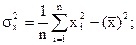
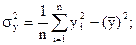
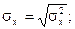
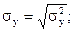(12)

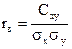(13)

- выборочный коэффициент корреляции, где 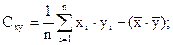- корреляционный момент.

Эмпирическое уравнение прямой линии регрессии X на У соответственно записывается в виде

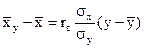. (14)

Обе прямые эмпирической регрессии пересекаются и проходят через точку
M( 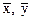), являющуюся центром распределения. Это две разные прямые. Эмпирические прямые регресси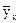и и 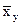совпадают только в случае линейной функциональной зависимости между СВ Х и У, т. е. |r| =1.

При проведении соответствующего расчета сначала определяется величина коэффициента корреляции r_в (-1 < r_в < 1). Пусть r_в ¹ 0. Коэффициент r_в вычисляется по данным выборки и, в отличии от коэффициента корреляции генеральной совокупности r, является случайной величиной. Для выяснения значимости r_в проверяется гипотеза Н₀ об отсутствии линейной корреляционной связи между СВ X и У, т.е. Н₀: r = 0.

При справедливости этой гипотезы статистика

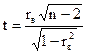(15)

имеет распределение Стьюдента с k = n- 2 степенями свободы. Гипотеза Н₀ отвергается, если |t| > t_{1-a; k}, где t_{1-a; k} - табличное значение распределения Стьюдента, определенное на уровне значимости a (1 - а = g, где g - доверительная вероятность) при числе степени свободы k= n- 2.

Таким образом, основной задачей корреляционного анализа является выявление связи между случайными величинами и оценка ее тесноты с помощью коэффициентов корреляции.

Установление формы зависимости и изучение зависимости между переменными является основной задачей регрессионного анализа.

Корреляционный анализ и регрессионный анализ является смежными, взаимосвязанными разделами математической статистики и предназначены для изучения по данным выборки статистической зависимости ряда величин.

Решение типового варианта инлдивидуального расчетного задания

Пример 1.

Дана выборка:

Для заданной выборки из генеральной совокупности СВ Х (n=100) необходимо: