Доверительные интервалы для оценки математического ожидания нормально распределенной СВ

Статистические оценки параметров неизвестного распределения по выборке 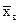, D_в и s_в называются точечными, так как определяются одним числом и указывают точку на числовой оси Ох. При небольшом объеме выборки пользуются интервальными оценками, поскольку точечная оценка 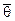может значительно отличаться от оцениваемого параметра q в генеральной совокупности.

Интервальные оценки определяются двумя числами - концами интервала, внутри которого с определенной вероятностью находится неизвестное значение параметра q.

Надежностью или доверительной вероятностью оценки величины q по 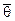называют вероятность , с которой осуществляется неравенство |q- 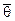|<d , где d>0. Чем меньше d, тем точность оценки выше. Величиной надежности g обычно задаются, полагая g =0,9; 0,95; 0,99 и др.

Пусть вероятность того, что |q- 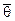|<d равна g , т.е. P(|q- 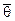|<d) = g, откуда следует

Р( 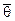-d <q< 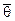+d)=g.

Интервал ( 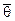-d; +d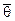), который покрывает (заключает в себе) неизвестный параметр q с заданной надежностью g, называется доверительным интервалом.

Пусть генеральная совокупность значений СВ X, из которой сделана выборка объема n, имеет нормальный закон распределения.

Нахождение доверительного интервала для неизвестного математического ожидания генеральной совокупности а=М(Х) при неизвестном s(X) проводится с использованием распределения Стьюдента (t -распределение случайной величины с числом степеней свободы k=n-l).

При заданной доверительной вероятности (надежности) g доверительный интервал находится из двойного неравенства

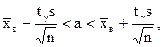
где 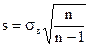- исправленное среднее квадратическое отклонение; n - объем выборки; t_g= t(g, n) - величина, значение которой определяется по специальным таблицам распределения Стьюдента в зависимости от объема выборки n и принятой надежности; s_в - выборочное среднее квадратаческое отклонение. Приведенная формула используется при любых выборках, в том числе и малых (n<30).