Проверка согласованности предложения о нормальном распределении генеральной совокупности по критерию Пирсона

Статистической гипотезой называют гипотезу о виде неизвестного закона распреде­ления или параметрах этого закона. Нулевой иди основной называют выдвигаемую гипотезу Н₀. Гипотезу H₁, которая противоречит нулевой, называют конкурирующей (альтернативой).

Нулевую гипотезу проверяют по имеющейся выборке, то есть по ограниченному числу данных, поэтому вывод о справедливости выполнения этой гипотезы может быть ошибочным.

В результате проверки статистической гипотезы возможны ошибки первого и второго рода.

Ошибка первого рода заключается в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что принимается неправильная гипотеза.

Вероятность ошибки первого рода называют уровнем значимости и обозначают a . Ее задают заранее малым числом, используя стандартные значения 0,01; 0,025; 0,05 и другие. Например, если принять a = 0,01, то это значит, что при проверке каждой из 100 выборок одинакового объема в среднем только в одном случае будет совершенна ошибка первого рода - отвергнута нулевая гипотеза Н₀. Вероятность ошибки второго рода обозначают через b.

Для проверки нулевой гипотезы Н₀ вводят в рассмотрение статистический критерий К - специально подобранную СВ, распределение которой изучено. При проверке гипотезы о нормальном распределении генеральной совокупности (объем выборки п > 50) обычно используют критерий «хи - квадрат» Пирсона.

Если Х₁, X₂,..., Х_n - независимые нормально распределенные нормированные СВ (имеют нулевые математические ожидания и единичные среднеквадрагические отклонения: М(Х) = 0, s(Х) =1), то закон распределения суммы квадратов этих величин

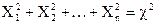(8)

называется распределением случайной величины «хи - квадрат» с n степенями свободы. Распределение c² рассчитано и табулировано. С увеличением числа степеней свободы оно медленно приближается к нормальному. Критические точки b = 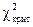в зависимости от уровня значимости a и числа степеней свободы рассматриваемой выборки приводятся в соответствующих таблицах.

Пусть имеется интервальный вариационный ряд, для которого вычислены 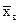и s_в, используя срединные значения интервалов .

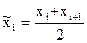Для того, чтобы при заданном уровне значимости a проверить гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона необходимо:

1. Пронормировать исследуемую СВХ, перейдя к случайной величине Z= 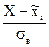, вычислить концы интервалов z_i= 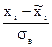, z_i+1= .

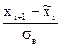При этом наименьшее значение z, т.е. z₁ (для первого интервала выборки) полагают равным –¥ , а наибольшее z (для последнего интервала), то есть z_k полагают равным + ¥.

2. Вычислить теоретические частоты 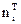. Для этого предварительно находят теоре­тические вероятности p_i » w_i попадания случайной величины X в интервал (х_i, x_i+1) по равенству p_i = Ф (z_i+1) - Ф (z_i), где значения нормированной функции Лапласа
Ф(х)= 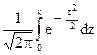берутся в соответствующих таблицах

Затем находятся теоретические частоты 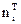=np_i.

3. Составить для сравнения таблицу значений эмпирических (опытных) частот n_i и теоретических частот 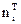. Если имеются интервалы, содержащие малочисленные частоты n_i <5 (обычно принадлежат крайним интервалом таблиц), то их следует объединить с соседними, а частоты этих интервалов сложить. Число окончательных интервалов группировки n_i и 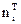обозначают S.

4. Найти наблюдаемое значение критерия Пирсона.

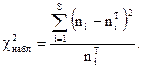(9)

5. Определить число степеней число свободы k = S-1-r (для нормального закона число параметров распределения г= 2).

6. Используя таблицу критических точек распределения c² по заданному a и найденному k определить критическую точку критической области 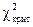(a, k). Возможный характер графика плотности вероятности СВ c² и положение критической точки показаны на рис.3 ( Р (c²> b}=a).

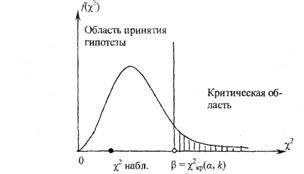
Рис.3

Если 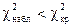, то нет оснований отвергать гипотезу о нормальном распределении заданной генеральной совокупности, в противном случае гипотезу отвергают.