Графическое представление вариационных рядов

Для наглядного представления вариационных рядов обычно используют изображение рядов в виде полигона или гистограмм.

Полигон служит для изображения дискретного вариационного ряда и представляет собой ломанную, в которой концы отрезков прямой имеют координаты (х_i, n_i), i=1,…m. Для ее построения используется ряд, приведенный в табл.1.

Гистограмма используется только для изображения интервальных рядов и имеет вид ступенчатый фигуры из прямоугольников с основаниями, равными длине интервалов h и высотами, равными частотам n_i интервалов (i =1,…k). Площадь такой гистограммы равна сумме всех частот n_i, т.е. объему выборки.

Для обоснования выбора возможного закона распределения генеральной совокуп­ности непрерывной СВ целесообразнее строить гистограмму относительных частот. С этой целью на оси Ох откладывают отрезки h, изображающие частичные интервалы варьирования. На этих отрезках, как на основаниях, строят прямоугольники с высотами, равными относительным частотам, поделенным на длину интервала 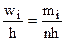(рис. 2).

Вероятностный смысл любого прямоугольника на гистограмме заключается в том. что его площадь 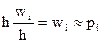, где р_i- вероятность попадания случайной величины в соответствующий интервал. Площадь всей гистограммы относительных частот равна единице, т.е. 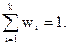. Для построения гистограмм используют данные табл.2.

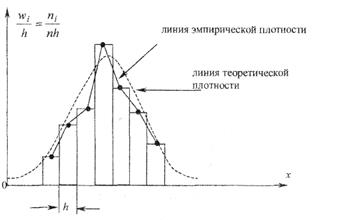
Рис.2

Соединив на полученной гистограмме середины верхних сторон прямоугольников получают линию эмпирической плотности (полигон относительных частот).

Гистограмма относительных частот и линия эмпирической плотности являются аналогами графиков плотности распределения f(x) непрерывных случайных величин, рассматриваемых в теории вероятностей. Сопоставляя их с графиками известных теоретических распределений f(x) можно выдвинуть предложение (гипотезу) о том, какому из теоретических распределений подчиняется генеральная совокупность рассматриваемой СВ.

Если линия эмпирической плотности близка по форме кривой Гаусса, то можно выдвинуть нулевую гипотезу о том, что генеральная совокупность подчиняется нормальному закону распределения вероятностей.