Определить размах варьирования случайной величины и составить вариационный ряд распределения.

По формуле Стерджеса определить длину интервалов и составить интервальный вариационный ряд.

3. Найти выборочную среднюю 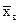, выборочную дисперсию D_в, выборочное среднее квадратическое отклонение s_в, моду М_о, медиану М_е;и коэффициент вариации d_в.

4. Построить эмпирическую функцию распределения вероятностей F*(x).

Решение

1. Объем выборки n =100. Определяем X_min=59, X_max=98. Размах варьирования R =39.

По значениям выборки Х составляем вариационный ряд

Таблица 1

x_i
m_i

x_i
m_i

x_i
m_i

x_i
m_i

2. Длину интервала находим по формуле Стерджеса

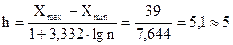. В качестве начала первого интервала возьмем a= 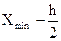=59-2,5=56,5.

Составим интервальный ряд распределения.

Таблица 2

Начало интервала Х_i	Конец интервала Х_i+1	Середины интервалов	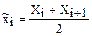Частоты m_i	Относительные частоты	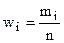Плотность частоты	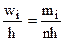Накоплен-ные частоты
56,5	61,5			0,03	0,0060	0,03
61,5	66,5			0,06	0,0120	0,09
66,5	71,5			0,14	0,0280	0,23
71,5	76,5			0,25	0,0500	0,48
76,5	81,5			0,2	0,0400	0,68
81,5	86,5			0,16	0,0320	0,84
86,5	91,5			0,1	0,0200	0,94
91,5	96,5			0,05	0,0100	0,99
96,5	101,5			0,01	0,0020	1,00

3. Находим выборочное среднее 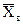, выборочную дисперсию 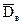и выборочное среднее квадратическое отклонение .

, ,

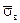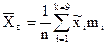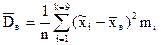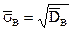
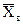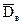Для контроля вычислений и исключения арифметических ошибок расчеты сумм, входящих в формулы и производим с помощью таблицы 3.

Таблица 3

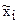
	m_i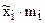
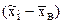
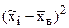
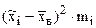
			-18,6	345,96	1037,88
			-13,6	184,96	1109,76
			-8,6	73,96	1035,44
			-3,6	12,96
			1,4	1,96	39,2
			6,4	40,96	655,36
			11,4	129,96	1299,6
			16,4	268,96	1344,8
			21,4	457,96	457,96
-	-	S=7760	-	-	S=7304

Последовательность заполнения таблицы 3.

1. Сначала заполняются первые три столбца, вычисляется

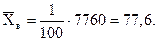
2. Заполняются следующие столбцы, вычисляется

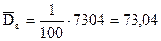, вычисляем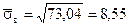

По данным таблицы 1 находим

Мода: М_о=69 и М_о=76 (самые частые значения).

Медиана: М_е=77 (среднее значение в вариационном ряду, т.е. пятидесятое).

Найдем коэффициент вариации

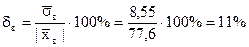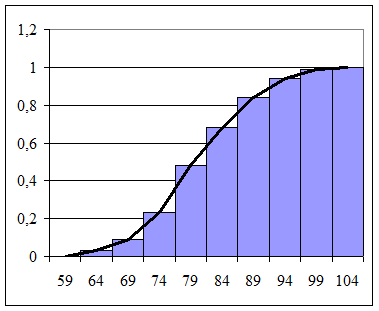
4. Найдем эмпирическую функцию распределения, используя данные таблицы №2.

			x £
	0,03		<x £
	0,09		<x £
	0,23		<x £
F^*(x)=	0,48		<x £
0,68		<x £
	0,84		<x £
	0,94		<x £
	0,99		<x £
	1,00		х>

Построим график этой функции

х

F^*(x)

Задание № 2. По данным предыдущего задания необходимо:

1. Построить гистограмму относительных частот и линию эмпирической плотности.

2. Пользуясь критерием Пирсона проверить гипотезу о нормальном законе распределения генеральной совокупности при уровне значимости a=0,05, предварительно вычислив для каждого интервала группирования вариационного ряда выравнивающие частоты.

3. На гистограмме относительных частот нанести линию теоретической плотности f(x) нормального распределения.

4. найти доверительный интервал для оценки неизвестного математического ожидания генеральной совокупности случайной величины с надежностью 0,95.

Решение:

1. Построим гистограмму относительных частот и линию эмпирической плотности. Для этого на каждом интервале из первого столбца таблицы 2 построим прямоугольник высотой w_i/h= w_i/5 и соединим середины верхних сторон прямоугольников.

x

w/h

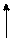
2. В качестве теоретического закона примем нормальный с плотностью распределения

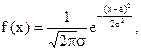и с параметрами а= 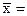77,6; s=8,56

Проверяем гипотезу о нормальном законе распределения случайной величины Х.

Теоретические (выравнивающие) частоты находим по формуле

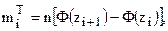
где Ф(z) – значения функции Лапласа,

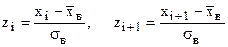
Составляем расчетную таблицу

Таблица 4

x_i	x_i+1	z_i	z_i+1	Ф(z_i)	Ф(z_i₊₁)	D_i=Ф(z_i₊₁)-Ф(z_i)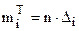
-¥	61,5	-¥	-1,8838	-0,5	-0,4702	0,0298	2,98
61,5	66,5	-1,8838	-1,2988	-0,4702	-0,4030	0,0672	6,72
66,5	71,5	-1,2988	-0,7138	-0,4030	-0,2623	0,1407	14,07
71,5	76,5	-0,7138	-0,1287	-0,2623	-0,0512	0,2111	21,11
76,5	81,5	-0,1287	0,4563	-0,0512	0,1759	0,2271	22,71
81,5	86,5	0,4563	1,0414	0,1759	0,3512	0,1752	17,52
86,5	91,5	1,0414	1,6264	0,3512	0,4481	0,0969	9,69
91,5	96,5	1,6264	2,2115	0,4481	0,4865	0,0384	3,84
96,5	+¥	2,2115	+¥	0,4865	0,5000	0,0135	1,35
						Sр_i=1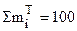

В последней строке таблицы №4 проведена проверка.

Проводим сопоставление эмпирических частот с теоретическими выравнивающими частотами.

Таблица 5.

m_i
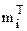
	2,98	6,72	14,07	21,11	22,71	17,52	9,69	3,84	1,35

Мы видим, что существует расхождение между опытными и теоретическими частотами. Необходимо выяснить, является ли это расхождение незначительным, или оно связано с тем, что мы неправильно выбрали закон распределения.

Объединяя малочисленные частоты на краях (<5), получим таблицу 6 с числом интервалов выборки S =5.

Таблица 6.

m_i
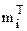
	9,70	14,07	21,11	22,71	17,52	9,69	5,19

Проверяем согласие гипотезы о нормальном законе распределения изучаемой случайной величины Х по критерию Пирсона. Для этого, пользуясь таблицей 6 вычислим величину

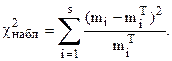
Заполним таблицу

Таблица 7

m_i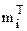
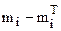
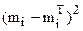
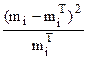
	9,70	-0,70	0,49	0,05
	14,07	-0,07	0,00	0,00
	21,11	3,89	15,13	0,72
	22,71	-2,71	7,36	0,32
	17,52	-1,52	2,32	0,13
	9,69	0,31	0,09	0,01
	5,19	0,81	0,65	0,13

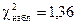
Проверим выполнение неравенства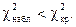

Пользуемся таблицей критических точек распределения c². Уровень значимости
a=0,05. Число степеней свободы k =S –3, где S –число интервалов выборки. Для нас
k =7–3=4. По таблице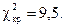

Так как 1,36 <9,5, то критерий выполняется, следовательно, гипотеза о нормальном законе принимается.

3. Для построения линии теоретической плотности найдем пять характерных точек:

1. Точка максимума

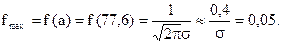
2. Точки перегиба

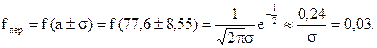
3. Практические нули (правило трех сигма)

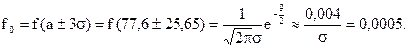
Нанесем линию на предыдущий рисунок.

4. Доверительный интервал для оценки математического ожидания найдем по формуле

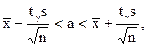
где 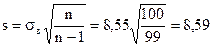, t_g находим по таблицам распределения Стьюдента t_g= t(g, n)= t(0,95, 100)=1,984

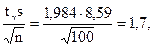
77,6-1,7<a<77,6+1,7

Окончательно

75,9<a<79,3

Пример 3. Для двумерной случайной величины (Х, У), представленной в корреляционной таблице 3, необходимо:

1. Определить выборочный коэффициент корреляции r_в;

2. Установить его значимость при доверительной вероятности g=0,95 (уровне значимости a =1-g =0,05);

3. В случае линейной корреляции между СВ Х и У найти выборочное уравнение прямой 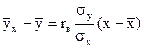регрессии У на Х;

4. На корреляционном поле парных зависимостей СВ Х и У нанести полученное уравнение прямой регрессии.

Решение:

1. Предварительно вычислим суммы

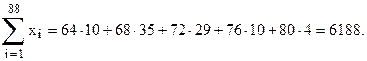
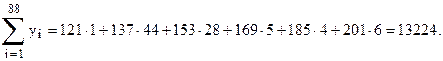
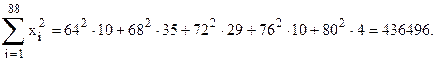
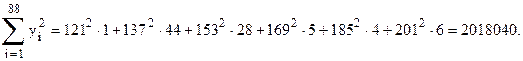
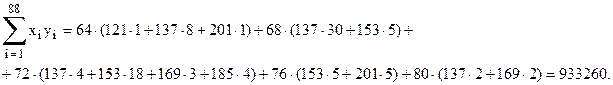
Средние арифметические значения

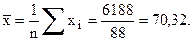
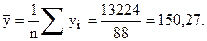
Дисперсии и средние квадратические отклонения

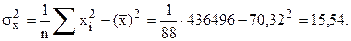
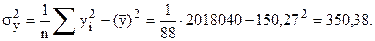
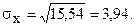
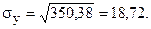
Найдем корреляционный момент

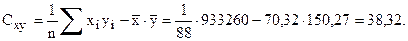
Находим коэффициент корреляции

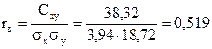
2. Приняв доверительную вероятность g=0,95 при n =88 и числе степеней свободы k=n-2=86 по таблице распределения Стьюдента определяем t_кр=t_{0,95; 86}=2,635.

Вычисляем статистику 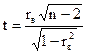= 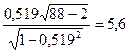Ж

Так как t>t_кр, то гипотезу об отсутствии линейной корреляции между СВ Х и Y отвергаем.

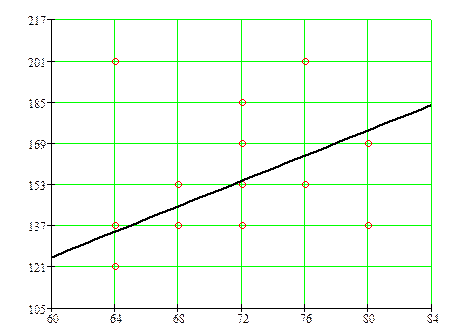
3. Находим уравнение линии эмпирической регрессии

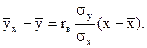Или

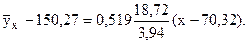Окончательно

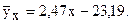
4. В системе координат х и у, используя корреляционную таблицу, соответствующими точками изображаем корреляционное поле и наносим прямую выборочной регрессии согласно полученного уравнения. На корреляционном поле цифрами показано количество совпадающих точек.

1 5

3 2

5 18 5

8 30 4 2

y

x