Построение линии теоретической плотности нормального распределения по опытным данным

Плотность распределения вероятностей нормального закона характеризуется двумя параметрами: математическим ожиданием М(Х) =а и средним квадратическим отклонением s. Она имеет вид

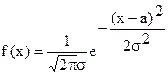(6)

График функции f(x) имеет вертикальную ось симметрии х = а.

Если положить а =0 и s=1, то кривая f(x) сдвинется вдоль оси, и ее осью симметрии станет ось ординат Оу. Такое нормальное распределение называется нормированным.

Обозначим (X-а)/s =u. Тогда формула плотности вероятностей принимает вид

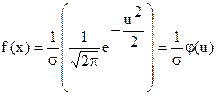(7)

Для нахождения значений j(u) обычно пользуются соответствующими таблицами функции j(u).

При построении линии теоретической плотности заданной выборки вместо а и s используют соответственно 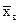и s_в. Сначала, полагая 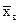х = и х = 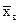±s_в, находят максимальное значение f(х) и значения этой функции в точках перегиба. Задавшись еще несколькими точками на оси Ох в пределах расположения гистограммы относительных частот находятся значения параметра u , по ним j(х) и, наконец, f(х). Полученные точки соединяют плавной кривой, которая будет симметричной относительно оси х = .

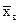График теоретической плотности следует изобразить на гистограмме относительных частот.