Двумерные выборки и парная регрессия

При исследовании по выборке зависимости между двумя СВ X и Y методами корреляционного анализа изучается усредненный закон поведения каждой из величин в соответствии со значениями другой величины, а также мера зависимости между ними.

Пусть мы имеем выборку n парных значений СВ X и У(х₁, у₁), (х₂, у₂),..., (х_n, у_n), представленных соответствующей таблицей, причем некоторые значения могут повторятся, или благодаря естественному разбросу экспериментальных данных одному значению переменной соответствует несколько значений другой. Для изучения по выборке общей картины корреляционной зависимости случайных величин X и У их парные значения наносятся соответствующими точками на координатной плоскости.

Такое изображение называется корреляционным полем. По нему делается вывод о том, линейную или нелинейную функциональные зависимости (эмпирические уравнения регрессии) следует искать между X и У (см. рис, 4а и 46), или она не существует (рис. 4в).

а)

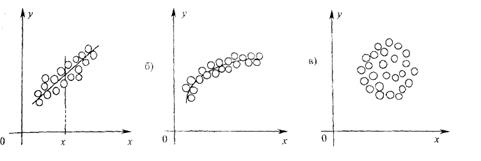
Рис. 4

При большом числе наблюдений (n ³50) для дальнейшего анализа корреляционной зависимости между СВХ и У обычно используют корреляционные таблицы. С этой целью варианты одной СВ, например X, записываются в первую строку таблицы, а варианты другой У в первый столбец. В соответствующую клетку на пересечении значений х_i, и y_i заносят частоты n_ху. Сумма nv по строкам и столбцам определяег соответствующие частоты n_х и n_у. Объем выборки .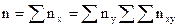

Если в корреляционной таблице остались пустые клетки, то это означает, что в выборке отсутствуют соответствующие сочетания значений СВ и X и У.

Ниже представлена подобная корреляционная таблица 3 системы двух случайных величин (X, У), используемая в дальнейшем при расчете типового примера.

Таблица 3

Зафиксируем конкретное значение одной случайной величины, например X = х (рис. 4а), тогда совокупность соответствующих значений другой СВ У можно рассматривать как отдельную случайную величину со своим законом распределения вероятностей и своими числовыми характеристиками, которые называют условными. В качестве оценок условных математических ожиданий таких величин принимают средние 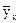, представляющие средние арифметические наблюдавшихся значений СВ У, соответствующих фиксированным значениями х.

Рассматривая эти средние значения СВ У при всех остальных значениях СВ X, можно получить эмпирическую (выборочную ) функцию регрессии У на X вида 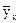=f(x). График этой функции называется эмпирической или выборочной линейной регрессией У на Х.

Аналогично, зафиксировав конкретные значения У = у и определяя по данным выборки или корреляционной таблицы условные средние 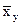, можно получить эмпирическую функцию регрессии X на У вида 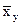= j(у) , которой будет соответствовать своя линия регрессии Х на У.

Задаваясь на основании построенного корреляционного поля видом линейной или нелинейной функции эмпирической регрессии, окончательные параметры уравнения устанавливают обычно методом наименьших квадратов. С этой целью проводится минимизация суммы квадратов отклонений от выбранной линии теоретической функции по вертикали, если ищутся параметры уравнения 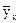=f(x), и по горизонтали для определения параметров уравнения 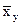= j(у).

Полученный график эмпирической функции регрессии на корреляционном поле будет наилучшим приближением ко всем экспериментальным точкам.