Теорема сложения математических ожиданий.

Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин.

Постановка задачи. Дана система случайных величин (X,Y), плотность распределения которой 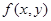известна. Требуется определить математическое ожидание суммы случайных величин M(Z)=M(X+Y).

Используя определение математического ожидания случайной непрерывной величины, получаем

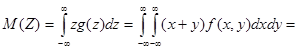
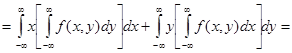
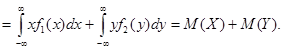Т.е. .

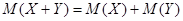Если случайная величина 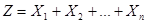, то 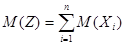. (4.1)

Эта теорема справедлива как для зависимых, так и для независимых величин.

Математическое ожидание линейной функции случайных величинравно той же линейной функции от математических ожиданий этих величин:

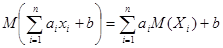, где 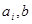- неслучайные величины.

В случае комплексного характера случайной величины 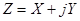математическое ожиданиеее также будет комплексным:

.

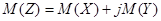Математическое ожидание произведениянескольких независимых случайных величин равно произведению математических ожиданий этих случайных величин.

Постановка задачи.

Пусть случайная величина 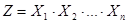имеет закон распределения 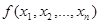. Требуется определить МО M(Z) случайной величины Z.

.

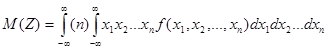Поскольку случайные величины 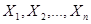являются независимыми, то функцию 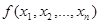можно представить как произведение сомножителей:

.

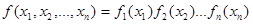Тогда математическое ожидание случайной величины Z будет равно

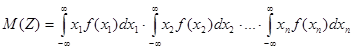. Откуда

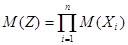. (4.2)

Выражение (4.2) не применимо для зависимых случайных величин.

Математическое ожидание произведения двух зависимых случайных величин равно сумме произведений их математических ожиданий и корреляционного момента:

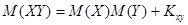. (4.3)

Справедливость этого свойства вытекает из формулы корреляционного момента.

Математическое ожидание нелинейной функции случайных аргументов.Пусть случайная величина Z является функцией случайных аргументов 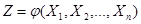. Требуется определить МО M(Z).

Поставленная задача решается точно только для некоторых частных случаев. В общем случае при решении этой задачи сначала нелинейную функцию в окрестности точки 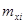линеаризуют разложением ее в ряд Тейлора:

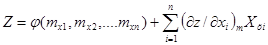. Применяя к этой случайной величине свойство МО линейной функции, находим:

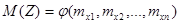, (4.4)

учитывая, что .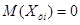

Таким образом, МО нелинейной функции случайных аргументов равно этой же функции от математических ожиданий этих аргументов.