Для системы случайных дискретных величин
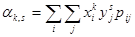 ,
,
где 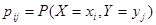 - вероятность того, что система (X, Y) примет значение
- вероятность того, что система (X, Y) примет значение  , а суммирование распространяется по всем возможным значениям случайных величин X и Y.
, а суммирование распространяется по всем возможным значениям случайных величин X и Y.
На практике чаще всего применяются начальные моменты первого порядка:
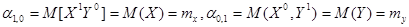 .
.
Они являются математическими ожиданиями случайных величин X и Y, входящих в систему и характеризуют положение системы, представляя собой координаты средней точки (центра рассеивания) системы на плоскости.
На основе определения начальных моментов можно записать формулы для математических ожиданий M(X) и M(Y) случайных величин X и Y, входящих в систему, в случае:
а) дискретных величин
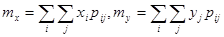 ,
,
Пример 5. Система двух случайных дискретных величин задана таблицей распределения:
| X1=3 | X2=6 | X3=9 | |
| Y1=4 | 0,1 | 0,2 | 0,3 |
| Y2=8 | 0,2 | 0,1 | 0,1 |
Найти математическое ожидание случайных величин X и Y, входящих в систему.
Решение.
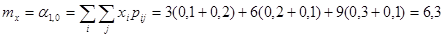 ;
;
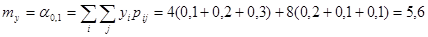 .
.
Вывод: центр группирования этой системы случайных величин находится в точке с координатами 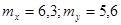 .
.
Центральные моменты системы.
Центральным моментом системы (X, Y) порядка k, s называют математическое ожидание произведения 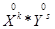 :
:
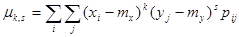 для дискретных величин и
для дискретных величин и
Среди центральных моментов большое практическое значение имеют вторые центральные моменты системы:
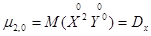 и
и 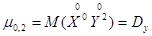 .
.
Эти моменты являются дисперсиями случайных величин X и Y, входящих в систему, и характеризуют рассеивание случайных точек в направлении осей 0x и 0y.
Формулы дисперсий случайных величин X и Y, входящих в систему,
а) для дискретных величин:
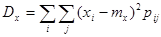 ;
; 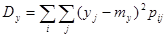 ,
,
Для характеристики системы случайных величин важную роль играет второй смешанный центральный момент
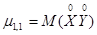 ,
,
т.е. математическое ожидание произведения центрированных величин.
Эта характеристика называется корреляционным моментомили ковариацией:
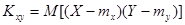 .
.
Корреляционный момент кроме рассеяния случайных величин X и Y характеризует еще и связь их между собой.
Корреляционный момент вычисляется по формуле:
а) для системы дискретных величин
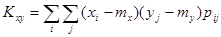 ;
;
При решении многих задач, в которых требуется определить корреляционный момент, удобнее пользоваться следующей формулой:
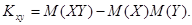
Она вытекает из определения корреляционного момента.
Дата добавления: 2021-11-16; просмотров: 416;











