Закон распределения суммы двух случайных величин.

При изучении тех или иных явлений приходится сталкиваться со случайными величинами, которые являются результатом суммирования некоторого числа случайных величин. Задача нахождения закона распределения суммы двух и более случайных величин может быть решена следующим образом.

Постановка задачи.

Пусть имеется система случайных величин (X,Y) с известной совместной плотностью распределения f(x,y).Требуется определить закон распределения случайной величины .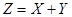

Для решения задачи обозначим функцию распределения случайной величины Z,как 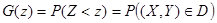и построим на плоскости x0y прямую x+ y=z, которая делит плоскость на две области (рис.4.1).

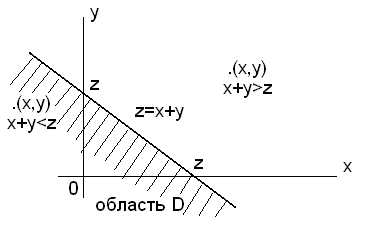
Рисунок 4.1 - График случайной величины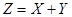

Заштрихованная область на рисунке является областью D.

Вероятность попадания случайной точки z в область D есть функция распределения случайной величины Z, которая по определению равна

.

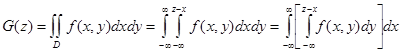Дифференцируя это выражение по переменной z, получим формулу плотности g(z) суммы двух случайных величин X и Y.

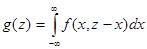. (4.12)

Аналогично можно получить и формулу плотности g(z), равную

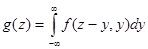, (4.13)

которая равносильна формуле (4.12) и может применяться вместо нее.

Если случайные величины X и Y независимы, то закон распределения суммы X+Y называется композицией законов распределения. В этом случае функции в формулах (4.12), (4.13) могут быть представлены в виде:

; .

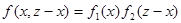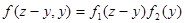Тогда плотность распределения g(z) будет окончательно равна:

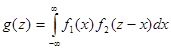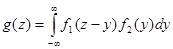; . (4.14)