Корреляционный момент. Коэффициент корреляции.

Для характеристики системы случайных величин важную роль играет второй смешанный центральный момент

,

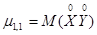т.е. математическое ожидание произведения центрированных величин.

Эта характеристика называется корреляционным моментомили ковариацией:

.

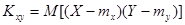Корреляционный момент кроме рассеяния случайных величин X и Y характеризует еще и связь их между собой.

Свойства корреляционного момента:

а) ;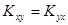

б) ;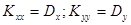

в) 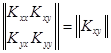- корреляционная матрица.

Для системы двух случайных величин числовыми характеристиками являются: .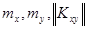

Из определения корреляционного момента следует, что размерность его равна размерности произведения случайных величин X и Y. Поэтому для одних и тех же величин значения его будут зависеть от единиц измерения случайных величин.

Эта особенность корреляционного момента является его недостатком, так как вызывает затруднения при сравнении корреляционных моментов различных пар случайных величин. Для устранения этого недостатка вводят новую числовую характеристику – коэффициент корреляции или нормированный корреляционный момент.

Коэффициентом корреляции 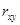случайных величин X и Y называют отношение корреляционного момента 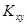к произведению средне – квадратичных отклонений этих величин:

.

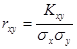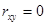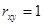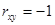Для независимых величин ; для величин, связанных между собой линейной зависимостью, или . Равенство нулю коэффициента корреляции еще не свидетельствует о том, что случайные величины являются независимыми.