Условное математическое ожидание. Уравнение линии регрессии.

Определение.Случайные величины являются связанными между собой, если при изменении одной из них другая реагирует изменением своего условного математического ожидания.

Условное математическое ожидание случайной непрерывной величины можно определить по формуле

,

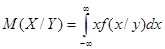где M(X/Y) - условное математическое ожидание случайной величины X при условии, что случайная величина Y приняла частное значение y.

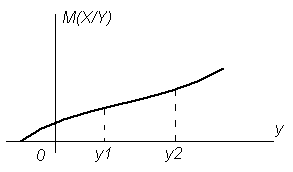
Рисунок 3.9 Графическая интерпретация условного математического ожидания M(X/Y)

Условное математическое ожидание M(X/Y) является функцией случайной величины Y (рис. 3.9). Если 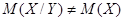, то случайные величины X и Y считаются связанными. Связанность случайных величин является частным случаем их зависимости.

На практике чаще всего M(X/Y) имеет вид прямой линии, которую называют линией регрессии, описываемой уравнением

.

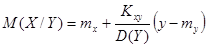Положение линии регрессии зависит от величины и знака корреляционного момента (рис. 3.10). Если значение корреляционного момента случайных величин X и Y меньше нуля, то регрессия отрицательная, а если значение корреляционного момента больше нуля, то регрессия положительная. Если значение корреляционного момента равно нулю, то случайные величины X и Y между собой не связаны.

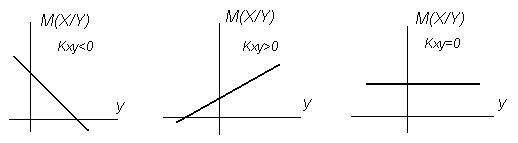
Рисунок 3.10 Положение линии регрессии в зависимости от величины и знака корреляционного момента