Композиция одномерных нормальных законов.

Найти плотность распределения композиции 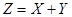нормально распределенных случайных величин X и Y с параметрами 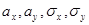, если

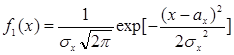и .

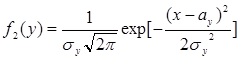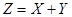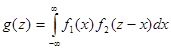Так как по определению плотность распределения композиции равна , то

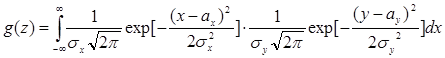. Откуда

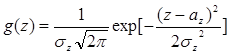, где 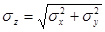, 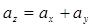. (4.16)

Следовательно, в результате композиции двух нормальных распределений суммарный закон получается также нормальным.

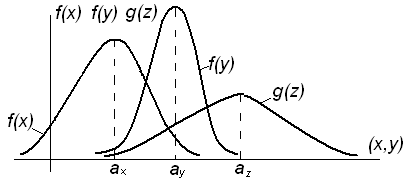
Рисунок 4.2 – Композиция двух нормальных распределений

При композиции произвольного числа нормальных распределений суммарный закон также является нормальным с параметрами:

; .

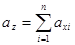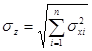Это свойство часто называют устойчивостью нормального закона.

Понятие о центральной предельной теореме.

Если случайные величины 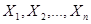взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием 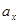и дисперсией 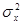, то при неограниченном увеличении n закон распределения суммы 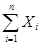неограниченно приближается к нормальному закону:

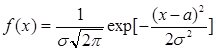с параметрам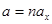и и .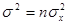

Теорема Ляпунова верна и для суммы случайных величин с неодинаковыми законами распределения, у которых дисперсии примерно одного порядка.