Виды математических утверждений

Будем рассматривать высказывания о математических объектах, т.е. произвольные математические утверждения, которым можно приписать значение истина или ложь. Например, “2´2=5”, “2´2=4” и “сумма углов треугольника равна 180⁰” – математические высказывания.

Несколько упрощая и огрубляя действительность, можно сказать, что любое математическое утверждение можно записать в одном из следующих видов: " х Р(х) или $ х Р(х), где х – некоторая переменная, а Р(х) – предикат (на самом деле переменных может быть несколько). В общем виде будем писать Q x P(x), подразумевая под Q один из кванторов (Q Î {", $}). Конечно, сам предикат Р(х) при этом может иметь сколь угодно сложную структуру.

Например, знакомое из анализа утверждение (" e > 0 ($ n Î N (" k, m Î N (k, m ³ n) ® |a_m – a_n| < e))) представляет собой критерий Коши сходимости последовательности {a_n}. Здесь в качестве переменной использован символ e, а предикат Р(e) – это достаточно сложное высказывание с переменной ($ n Î N (" k, m Î N (k, m ³ n) ® |a_m – a_n| < e)) . На самом деле это высказывание правильно записать так: ($ n Î N (" k, m Î N (k ³ n) Ù (m ³ n) ® |a_m – a_n| < e)) . Таким образом, исходное утверждение состоит из кванторной приставки " e > 0 $ n Î N " k, m Î N и условия (k ³ n) Ù (m ³ n) ® |a_m – a_n| < e , имеющего вид импликации двух пре­ди­катов: одного – (k ³ n) Ù (m ³ n) и второго – |a_m – a_n|<e. Эти предикаты сами используют другие предикаты ³ , < и знаки функций – ведь последовательность – это функция, сопоставляющая каждому натуральному числу n значение а_n . Ещё более формально критерий Коши следует писать так:

" e ($ n (" k (" m((e Î R Ù e > 0) Ù (n Î N) Ù (kÎ N Ù k ³ n) Ù (mÎ N Ù m ³ n)® |a_m – a_n| < e)))).

Здесь " e $ n " k " m – кванторная приставка, а всё остальное – высказывание с переменными, т.е. предикат, образованный с помощью логических связок из более простых предикатов e Î R , e > 0 , n Î N , kÎ N , mÎ N , k ³ n, m ³ n, |a_m – a_n| < e .

Как правило, встречающиеся математические утверждения можно записать в аналогичном виде: (кванторная_приставка) (предикат_1 ® предикат_2). Такая запись называется импликативной формой записи математического утверждения (т.к. в ней используется импликация).

Сразу напрашивается возражение: теорема Пифагора формулируется совсем иначе – ква­драт гипотенузы равен сумме квадратов катетов – где же тут импликация ? Просто при­ве­дённая формулировка не является строгой: например, в ней совсем не упоминается пря­мо­угольный треугольник, не ясно также, что такое его гипотенуза и катеты. Импликативная форма запи­си выглядит, например, так: " D АВС ((Ð АСВ = 90⁰) ® АВ² = АС² + ВС²). Здесь " D АВС – кванторная приставка, Ð АСВ = 90⁰ – предикат_1, АВ² = АС² + ВС² – предикат_2. Если опу­ститься (а может быть, подняться ?!) на ещё более высокую ступень формализма, то сле­дует ввести множество D всех треугольников и функции Ð С(х), АВ(х), ВС(х), АС(х), сопос­та­в­ляющие каждому треугольнику х = D АВС соответственно величину угла С и длины сто­рон АВ, ВС, АС. Тогда теорема Пифагора станет ещё более загадочной: " х Î D ((Ð С(х)=90⁰) ® АВ(х)² = АС(х)² + ВС(х)²).Хотя это и не предел формализации, но, как пра­вило, мы не будем забредать слишком далеко в подобные формалистические дебри.

Другой пример преобразования неимпликативного утверждения в импликативную форму: утверждение “1 является минимальным натуральным числом” может быть записано в импликативной форме так: " n (n Î N ® n ³ 1).

Упражнение: Преобразовать в импликативную форму и записать в виде формул с кванторами и предикатами следующие утверждения:

1) Сумма углов n-угольника равна (n–2)×p,

2) Квадрат действительного числа неотрицателен,

3) Натуральное число m делится на 12 тогда и только тогда, когда оно делится на 3 и на 4 ,

4) Если последовательность сходится, то сходится и её подпоследовательность с чётными номерами,

5) Диагонали параллелограмма делятся в точке пересечения пополам.

В дальнейшем ограничимся рассмотрением только простейших утверждений вида Q x (P(x) ® R(x)). По ним можно образовать следующие утверждения:

Q x (R(x)® P(x)), Q x ( ), Q x ( ),

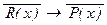которые называются соответственно обратным, противоположными контрапозиционным утверждениямик исходному. При этом само исходное утверждение Q x (P(x)® R(x)) называют прямым. Легко видеть, что контрапозиционное утверждение является противоположным к обратному, а утверждение обратное к обратному будет прямым, так же как и противоположное к противоположному.

Примеры: 1. Рассмотрим утверждение “если натуральное число n делится на 6, то оно делится на 2 и на 3”. Его импликативная форма:

" n Î N ((n M 6) ® (n M 2) Ù (n M 3))

– это прямое утверждение. Сформулируем другие виды утверждений:

обратное: " n Î N ((n M 2) Ù (n M 3) ® (n M 6)) – “если натуральное число n делится на 2 и на 3, то оно делится на 6”;

противоположное: " n Î N ((n 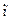6) ® (n 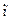2) Ú (n 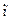3)) – “если натуральное число n не делится на 6, то оно не делится на 2 или на 3”;

контрапозиционное: " n Î N ((n 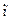2) Ú (n 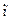3) ® (n 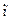6)) – “если натуральное число n не делится на 2 или на 3, то оно не делится на 6”.

2.Для прямого утверждения “если последовательности {a_n} и {b_n} сходятся, то сходится последовательность {a_n + b_n}” обратное звучит так: “если сходится последовательность {a_n + b_n}, то последовательности {a_n} и {b_n} сходятся”, противоположное – “если одна из последовательностей {a_n} или {b_n} не сходится, то не сходится последовательность {a_n + b_n}” и контрапозиционное – “если не сходится последовательность {a_n + b_n}, то одна из последовательностей {a_n} или {b_n} не сходится”.

Упражнение.Сформулировать все виды утверждений для прямых утверждений из предыдущего упражнения.

Каждое математическое утверждение, будучи высказыванием, является истинным или ложным. Поэтому для проверки истинности утверждения необходимо сопоставить его смысл с “окружающей математической действительностью” в самом широком смысле. Для доказательства истинности утверждения вида $ х Р(х) (не обязательно в импликативной форме) нужно найти хотя бы один объект а Î D(P) со свойством Р(a), т.е. хотя бы один элемент из области истинности предиката Р(х): а Î D₁(P). Для доказательства истинности утверждения вида " х Р(х) нужно проверить, что для любого объекта а Î D(P) выполнено свойство Р(a), т.е. доказать равенство D(P) = D₁(P).

Ложность утверждения вида Q x Р(х) равносильна истинности утверждения 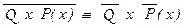, где 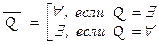(см. основные равносильности с кванторами). Поэтому проверка ложности математического утверждения сводится к проверке истинности некоторого другого утверждения аналогичной структуры.

Примеры: 1. Истинно ли утверждение $ х Î Z (" y Î R x×y = 3) ?

Пусть х = х₀ Î Zфиксировано. Рассмотрим высказывание " y Î R x₀×y = 3.

Очевидно, что оно ложно, т.к. при у = 0 условие х₀×у = 3 не выполнено ни при каком х₀ Î Z. Поэтому исходное утверждение ложно.

2.Истинно ли утверждение " х Î N ($ y Î R x×y = 3) ?

Пусть х = х₀ Î N фиксировано. Рассмотрим высказывание $ y Î R x₀×y = 3 . Поскольку х₀ Î N, а значит, х₀ ¹ 0, то это высказывание равносильно утверждению $ y Î R y = 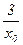, которое, очевидно, истинно (у явно вычислено по х₀). Поэтому исходное утверждение истинно.

3.Истинно ли утверждение " х Î N (" y Î N x×y + 1 > x + y) ?

Для х = х₀ Î Nрассмотрим высказывание " y Î N (x₀×y + 1 > x₀ + y) , которое при х₀ = 1 принимает вид " y Î N y + 1 > 1 + y и является ложным. Значит оно истинно не для любого х₀ Î N, т.е. исходное утверждение ложно.

Упражнение.Найдите истинные и ложные утверждения из предыдущего упражнения.

Совершенно не обязательно, что истинность прямого утверждения влечёт истинность и дру­гих – обратного, противоположного и контрапозиционного. Например, утверждение " т, n Î N (m | n ® m £ n) истинно, но обратное к нему: " т, n Î N (m £ n ® m | n) ложно, как и противоположное " т, n Î N (m 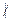n ® m > n); контрапозиционное утверждение " т, n Î N (m > n ® m 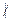n) снова истинно.

На самом деле контрапозиционное утверждение Q x ( 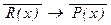) и прямое Q x (P(x) ® R(x)) всегда равносильны, т.е. истинны или ложны одновременно. Это следует из известного закона контрапозиции (a ® b) « ( 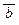® 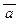). Эту равносильность иногда удобно использовать при доказательствах теорем: вместо прямого утверждения иногда удобнее доказывать контрапозиционное к нему.

Если прямое утверждение Q x (P(x) ® R(x)) истинно, то истинна импликация P(x) ® R(x) для некоторой совокупности объектов х (по крайней мере, для одного, если Q = $, и для всех, – если Q ="). Особое внимание уделим случаю Q =". Тогда предикат P(x) ® R(x) тождественно истинен, и вместо записи " x (P(x) ® R(x)) иногда кратко пишут Р(х) Þ R(x).При этомпредикат Р(х) называется достаточным условиемдля R(x), а предикат R(x) – необходимым условиемдля Р(х) или логическим следствием предикатаР(х). Смысл названий состоит в том, что для любого объекта а для проверки истинности условия R(а) достаточно проверить истинность условия P(а), а для того, чтобы Р(а) было истинным, необходимо (т.е. обязательно требуется), чтобы истинным было высказывание R(а), истинность которого следует из истинности Р(а).

Если предикаты Р(х) и R(x) равносильны, т.е. " х (P(x) « R(x)), то иногда кратко пишут Р(х) Û R(x).Ввиду равносильности " х (P(x) « R(x)) º º " х ((P(x)® R(x)) Ù (R(x)® P(x))), условие R(x) не только необходимо, но и достаточно для Р(х), а Р(х), в свою очередь, необходимо для R(x) и является логическим следствием предиката R(x). Вот почему вместо Р(х) Û R(x) часто говорят “условие Р(х) необходимо и достаточно для выполнения R(x)”. Ясно, что Р(х) Û R(x) º (Р(х) Þ R(x)) Ù (R(x) Þ Р(х)) поэтому вместе с прямым утверждением в этом случае справедливо и обратное.

Примеры: 1. Условие R(х) º “натуральное число х делится на 2” является необходимым условием для Р(х) º “натуральное число х делится на 6”, т.к. высказывание Р(х) Þ R(x) (º " х (P(x)® R(x))) истинно. Обратное утверждение R(x) Þ Р(х) в данном случае не верно, т.к. например, 2M 2, но 2 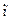6. Таким образом, условие R(х) необходимо, но не достаточно для Р(х).

2.Очевидно, что необходимым и достаточным условием для Р(х) º “натуральное число х делится на 6” является условие S(х) º “натуральное число х делится на 2 и на 3”. Таким образом, в этом случае справедливо Р(х) Û S(x).

Упражнение: Среди нижеследующих условий выделить необходимые, достаточные и необходимые и достаточные:

1) Р(х) = “два угла треугольника х и две его стороны равны между собой”, R(x) = “треугольник х равносторонний”,

2) Р(х) = “два угла треугольника х равны между собой”,

R(x) = “треугольник х равнобедренный”,

3) Р(х) = “три медианы треугольника х равны между собой”,

R(x) = “треугольник х равносторонний”,

4) Р(х) = “х Î N и х ³ 5”, R(x) º “х Î N и 2^х > 5”,

5) Р(х) º “х Î N и х ³ 5”, R(x) º “х Î N и 2^х > 5×х + 6”,

6) Р(х) º “последовательность {x_n} сходится”,

R(x) º “последовательность {x_2×n} сходится”,

7) Р(х) º “последовательность {x_n} сходится”,

R(x) º “последовательность {2×x_n} сходится”.