Интервальные оценки параметров распределения. Доверительный интервал.

Если случайная величина X подчинена нормальному закону, то для оценки параметров и проверки различных гипотез относительно этих параметров необходимо знание точного распределения некоторых выборочных характеристик. Например, для нахождения распределения эмпирической дисперсии необходимо исследовать распределение характеристик случайной величины, представляющей собой сумму квадратов n независимых случайных величин 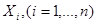, каждая из которых подчиняется нормальному закону с параметрами a=0 и .

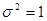Распределение случайной величины, удовлетворяющей этим условиям, называют хи–квадрат распределением или 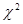- распределениемс k=n степенями свободы.

Число степеней свободы равно числу независимых переменных минус число связей, накладываемых на эти переменных. Если величины 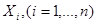связаны одним линейным соотношением, например, 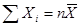, то число степеней свободы k=n-1.

Дифференциальная функция 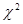- распределения для нее имеет вид

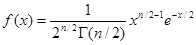при x>0, f(x)=0 при x<=0. Здесь

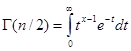- гамма – функция.

В частности, если x=n, то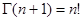

Для дифференциальной функции 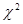- распределения из-за ее сложности составлены таблицы, позволяющие вычислять вероятности 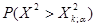, того, что случайная величина, распределенная по закону 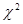с известным числом степеней свободы k, превысит некоторое фиксированное значение .

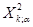График плотности вероятности - распределения при числе степеней свободы n=1, 2 и 6 изображен на рис. 5.3.

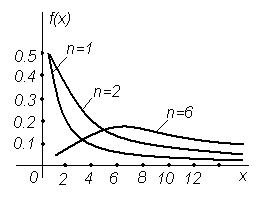
Рисунок 5.3 - График плотности вероятности - распределения

Распределение статистики 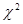не зависит ни от математического ожидания случайной величины X, ни от дисперсии, а зависит лишь от объема выборки n. Если случайная величина имеет 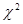распределение с k=n степенями свободы, то математическое ожидание и дисперсия соответственно равны: .

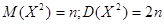Пример. Случайная величина имеет 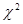- распределение с числом степеней свободы 5. Найти отклонение 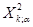, вероятность превышения которого равна 0.2.

Решение.

Из условия задачи следует, что надо найти такое значение 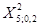, чтобы выполнялось равенство .

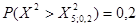Искомое значение 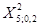ищется на пересечении строки 5 и столбца 0,2 таблицы (приложение). Оно равно 7,3, поэтому .

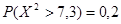Распределение 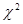обладает тем свойством, что сумма величин 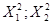, распределенные по закону 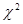со степенями свободы равными 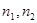, также распределена по закону 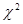с 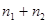степенями свободы.

При решении многих задач статистики приходится иметь дело со случайными величинами, имеющими так называемое распределение Стьюдента или t-распределение. Это же распределение применяется при нахождении оценки отклонения выборочного среднего от центра нормального распределения.

Распределение Стьюдента имеет случайная величина

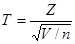, где Z – случайная величина, распределенная по нормальному закону с параметрами a=0 и 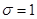; V – независимая от Z случайная величина, распределенная по закону 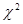с k=n степенями свободы.

Дифференциальная функция распределения Стьюдента имеет вид

.

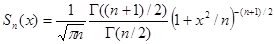Распределение Стьюдента обладает тем свойством, что с возрастанием числа степеней свободы оно быстро приближается к нормальному распределению (рис.5.4).

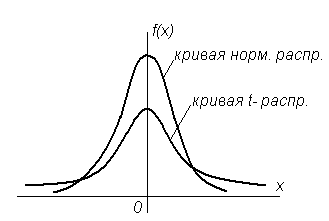
Рисунок. 5.4 – Графики нормального распределения и t - распределения

Доверительные границы для средних.Статистические оценки параметров распределения генеральной совокупности, рассмотренные ранее, являются точечными оценками. Если объем выборки невелик, то точечная оценка параметра может значительно отличаться от самого параметра. Поэтому в этих случаях применяют интервальную оценку. Задача интервальной оценки заключается в том, что по данным выборки строится такой числовой интервал (доверительный интервал), внутри которого с заранее заданной вероятностью, близкой к единице, будет находиться оцениваемый параметр.

Пусть для неизвестного параметра a найдена оценка 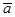и задана вероятность 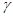, близкая к единице (доверительная вероятность). Требуется найти такое значение 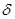, чтобы интервал 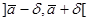длины 2 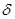накрыл искомое значение параметра a с вероятностью (надежностью) 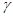, иначе говоря, выполнялось равенство

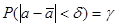или .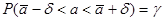

Безусловно, чем меньше длина интервала, тем точнее оценка искомого параметра a. При этом выбор доверительной вероятности (надежности) не является математической задачей, а определяется условиями задачи.

Например, пусть на двух предприятиях вероятность выпуска стандартных изделий равна 0,99, т.е. вероятность бракованных изделий равна q=0,01. Мала или велика эта вероятность? Для ответа на этот вопрос необходимо знать характер выпускаемой продукции. Пусть одно предприятие выпускает гвозди, а другое – парашюты. Если из 100 гвоздей один окажется бракованным, то с этим в какой-то степени можно мириться. Если же из каждых 100 парашютов один будет бракованным, то это может привести к многочисленным несчастным случаям, что недопустимо.