Элементы математической статистики. Генеральная и выборочная совокупности. Статистическое распределение выборки.
При изучении качественного и количественного признака, характеризующего множество некоторых однородных элементов, не всегда имеется возможность исследовать каждый из них. Поэтому в целях получения информации об этом множестве исследуют только некоторую небольшую часть ее элементов, отобранных совершенно случайно. Практика подтверждает, что выводы, сделанные в результате анализа этой части элементов, бывают достаточно объективными и для всего изучаемого множества.
Множество всех элементов, подлежащих изучению, называют генеральной совокупностью. В отличие от нее выборка – конечная совокупность элементов, отбираемых из генеральной совокупности, для статистического вывода о свойствах генеральной совокупности на основании свойств отобранных элементов.
Любое статистическое исследование всегда связано с производством выборки. Выборка должна быть представительной, т.е. такой, чтобы любой элемент генеральной совокупности мог попасть в нее с вероятностью, не зависящей от характеристик подлежащих измерению.
Число элементов генеральной совокупности (выборки) называют ее объемом.
Пример 1.Из партии, содержащей 10000 деталей, отобрали случайным образом для проверки 80 деталей.
Объем генеральной совокупности в данном примере равен 10000, а объем выборки – 80.
Очевидно, что чем больше объем выборки, тем более полное представление можно получить о генеральной совокупности.
Исследование выборки сводится к отысканию ее статистик (функций выборки), к которым относят: вариационный ряд, статистическое распределение выборки, эмпирическую функцию распределения, гистограмму, среднее арифметическое результатов наблюдений и т. п.Статистики, используемые для приближенной оценки параметров генеральной совокупности, называют также статистическими оценками.
Статистическое распределение выборки отражает соответствие между наблюдаемыми значениями и их частотами или относительными частотами.
Пусть из генеральной совокупности извлечена выборка объема n, причем 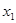 наблюдалось
наблюдалось 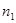 раз,
раз, 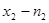 раз, …,
раз, …, 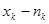 , где
, где 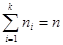 .
.
Наблюдаемые значения 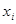 называют вариантами, последовательность же вариантов, расположенных в возрастающем порядке, - вариационным рядом.
называют вариантами, последовательность же вариантов, расположенных в возрастающем порядке, - вариационным рядом.
Число 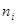 , показывающее, сколько раз встречается вариант
, показывающее, сколько раз встречается вариант 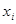 в выборке, называют частотой варианта.
в выборке, называют частотой варианта.
Отношение частоты варианта 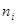 к объему выборки n называют относительной частотой:
к объему выборки n называют относительной частотой: 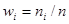 .
.
С учетом этих определений под статистическим распределением выборки понимают перечень вариант 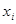 и соответствующих им частот
и соответствующих им частот 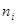 или относительных частот
или относительных частот 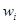 .
.
Пример 2Задано статистическое распределениечастот (Таблица 5.1):
Таблица 5.1
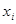
| |||
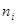
|
Объем выборки n=10. Находим относительные частоты:
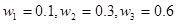 и составляем статистическое распределение относительных частот (таблица 5.2):
и составляем статистическое распределение относительных частот (таблица 5.2):
Таблица 5.2
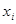
| |||
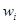
| 0.1 | 0.3 | 0.6 |
В целях наглядности соответствия между наблюдаемыми вариантами и частотами или относительными частотами распределение выборки изображают графически.
Для этого точки 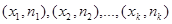 последовательно соединяют отрезками прямой. Получающаяся при этом ломаная линия называется полигоном частот; если же последовательно соединить отрезками прямой точки
последовательно соединяют отрезками прямой. Получающаяся при этом ломаная линия называется полигоном частот; если же последовательно соединить отрезками прямой точки 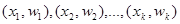 , то – полигоном относительных частот.
, то – полигоном относительных частот.
Дата добавления: 2021-11-16; просмотров: 495;











