Агрегированные оценки

Эксперт	Правило комбинирования свидетельств
Демпстер	Инагаки	Жанг	Ягер
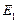
	0,10494	0,10495	0,067011	0,21149
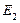
	0,12754	0,12304	0,32522	0,24859
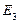
	0,072137	0,068686	0,051066	0,20631
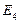
	0,12138	0,11924	0,071868	0,23047
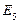
	0,11218	0,10995	0,06414	0,22504
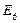
	0,097312	0,087752	0,11443	0,25379
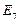
	0,13859	0,13824	0,11644	0,23313
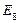
	0,07911	0,071313	0,057322	0,22677
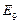
	0,098169	0,094506	0,038039	0,22354
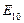
	0,074279	0,066168	0,096547	0,2281

Расчеты, выполненные на основе различных правил комбинирования свидетельств позволяют сделать следующие выводы:

1. По результатам представленным в табл. 3.22 и 3.23 наибольшие значения функции доверия и правдоподобия принадлежат выбору {E₇}, не зависимо от примененного правила комбинирования, но степень доверия, рассчитанная на основе различных правил отличается.

2. Степень доверия, назначенная выбору (эксперту) {E₇} находится в пределах от 0,0017 до 0,433.

3. Уровень конфликта варьируется в пределах от 0,36 до 0,65 в зависимости от правила комбинирования, что свидетельствует о наличии некоторого конфликта между отдельными группами свидетельств.

4. Суммарное значение всех масс вероятности выделенных фокальных элементов больше массы вероятности, относящейся к основе анализа ( , ).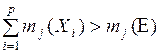

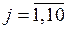5. Суждения ЛПР можно считать совместимыми.

Все выше перечисленные рассуждения позволяют сделать вывод о том, что наиболее эффективным правилом для рассмотренного примера может считаться правило Инагаки.

В результате проведенных расчетов были получены нормированные значения коэффициентов компетентности экспертов, которые соответственно равны 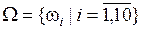={0,105; 0,13; 0,069; 0,12; 0,11; 0,09; 0,14; 0,07; 0,1; 0,066}.

На основании значений вектора Ω можно получить ранжировку экспертов, на основе рассчитанных значений коэффициентов компетентности, вида:

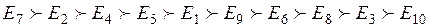
Эксперт E₇ признан наиболее компетентным в экспертной группе (по решению рассматриваемой задачи), эксперт E₁₀ признан наименее компетентным в группе.