Интервальная оценка среднеквадратического отклонения нормального распределения.
Задача построения доверительного интервала для оценки среднего квадратичного отклонения нормального распределения, покрывающего параметр 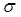 с заданной надежностью
с заданной надежностью 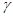 по исправленному среднему квадратичному отклонению s.
по исправленному среднему квадратичному отклонению s.
Решение задачи сводится к нахождению такого числа 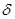 , чтобы выполнялось равенство
, чтобы выполнялось равенство
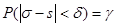 или
или 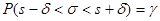 .
.
Для того чтобы можно было пользоваться готовой таблицей, преобразуем двойное неравенство 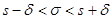 в равносильное неравенство
в равносильное неравенство
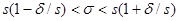 .
.
Обозначив 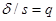 , получим
, получим
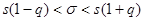 . (5.8)
. (5.8)
Таким образом, задача построения искомого доверительного интервала свелась к нахождению величины q.
Не вдаваясь в детали, отметим, что для этой цели вводится случайная величина X, равная
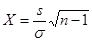 ,
,
дифференциальная функция которой имеет вид
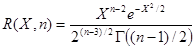 .
.
Для нахождения доверительной вероятности используется формула
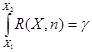 , где
, где 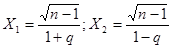 .
.
Из равенства (5.8) по заданному n и 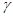 находится значение
находится значение 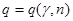 .
.
Функция 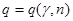 табулирована.
табулирована.
Следовательно, для построения искомого доверительного интервала достаточно по таблице найти соответствующее значение функции 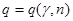 , а затем в двойное неравенство
, а затем в двойное неравенство 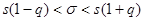 подставить значения s и q.
подставить значения s и q.
Пример. Построить доверительный интервал, покрывающий генеральное среднее квадратичное отклонение 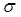 с надежностью
с надежностью 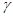 , если по выборке объема n найдено исправленное среднее квадратичное отклонение s:
, если по выборке объема n найдено исправленное среднее квадратичное отклонение s:
а) 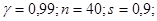
б) 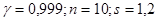 .
.
Решение.
По таблице значений функции 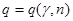 находим:
находим:
а) 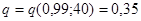 ; искомый доверительный интервал будет
; искомый доверительный интервал будет
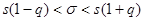 ;
; 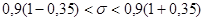 или
или
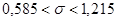 .
.
б) 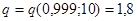 ; искомый интервал будет
; искомый интервал будет 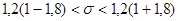 или
или 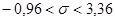 .
.
Так как среднее квадратичное отклонение 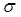 всегда положительно, то окончательно получим, что
всегда положительно, то окончательно получим, что 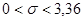 .
.
Дата добавления: 2021-11-16; просмотров: 689;











