Функция распределения системы случайных величин и ее свойства.
Функцией распределения системы двух случайных величин (X, Y) называется функция двух аргументов F(X, Y), равная вероятности совместного выполнения двух неравенств: X<x, Y<y, где x и y – действительные числа:
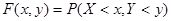 .
.
Функция распределения системы двух случайных величин геометрически представляет собой вероятность попадания случайной точки (X, Y) в бесконечный квадрант с вершиной (x, y), расположенный левее и ниже этой вершины (рис. 3.3).
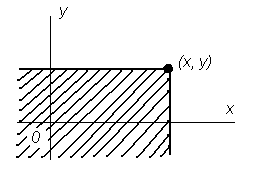
Рисунок 3.3 Геометрическая интерпретация функции распределения системы двух случайных величин
Геометрическая интерпретация функции распределения двумерной
случайной величины позволяет наглядно иллюстрировать ее свойства:
а) если один или оба аргумента стремятся к минусу бесконечности, то функция распределения стремится к нулю, т. е.
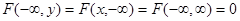 ;
;
б) если один из аргументов стремится к плюсу бесконечности, то функция распределения системы стремится к функции распределения одной случайной величины, соответствующей другому аргументу, т.е.
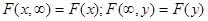 ;
;
в) если оба аргумента стремятся к плюсу бесконечности, то функция распределения системы стремится к единице
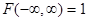 ;
;
г) функция распределения является неубывающей функцией по каждому аргументу, т.е.
если 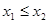 , то
, то 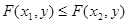 ;
;
если 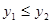 , то
, то 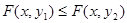 .
.
Дата добавления: 2021-11-16; просмотров: 542;











