Интервальная оценка математического ожидания нормального распределения при известном среднем квадратичном отклонении.

Задача построения доверительного интервала для оценки математического ожидания нормального распределения при известном среднем квадратичном отклонении 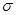сводится к следующему.

Обозначим неизвестное математическое ожидание через a, оценку же для него - .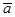

Для нормального распределения

; ; .

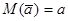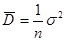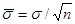Найдем доверительный интервал, покрывающий неизвестный параметр a с надежностью 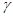, т.е. найдем такое 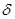, чтобы выполнялось равенство

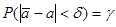. (5.6)

Для этого воспользуемся формулой

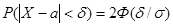, где Ф(x) – интеграл вероятности.

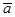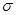Заменив в ней X на и на 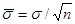, получим

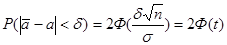, где .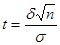

На основании равенства (5.6) можем записать, что

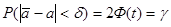, отсюда .

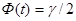Число t определяется по таблице значений функции Лапласа. Затем из соотношения 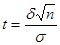находится оценка 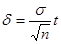. С учетом этого доверительный интервал будет

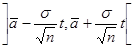. (5.7)

Пример. Случайная величина X имеет нормальное распределение с известным средним квадратичным отклонением 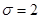. Построить доверительный интервал для неизвестного математического ожидания соответствующий доверительной вероятности 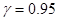, если объем выборки n=25.

Решение.

Найдем t из соотношения 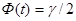. По таблице значений функции Лапласа находим t, соответствующее значению Ф(t)=0.95/2=0.475. Оно будет t=1.96.

Определяем точность оценки

.

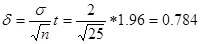Следовательно, доверительный интервал будет

.

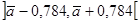Полученный результат говорит о том, что этот доверительный интервал покрывает неизвестное математическое ожидание a с вероятностью 0,95.