Теорема умножения вероятностей.
Вероятность произведения двух событий равна произведению вероятности появления одного из них на условную вероятность появления другого события.
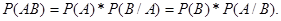
Доказательство.
Пусть опыт сводится к схеме случаев.
Пусть опыт имеет n элементарных равновозможных исходов, из которых событию A благоприятными являются m исходов, событию B - k исходов, а событию AB - l исходов, тогда
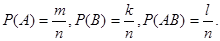
Из m исходов, в которых наступает событие A, благоприятных событию B, будет l исходов, поэтому условная вероятность события B равна
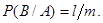
Аналогично из k исходов, в которых наступает событие B, благоприятных событию A, также будет l исходов, поэтому условная вероятность события A равна
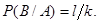
Отсюда произведения вероятностей
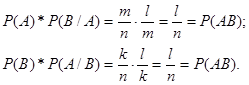
Из этих выражений следует справедливость теоремы.
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
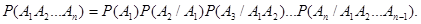
Частный случай теоремы умножения вероятностей: если события независимы, то вероятность произведения событий равна произведению вероятностей этих событий
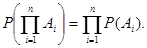
Доказательство:
Пусть события A и B независимы между собой, тогда
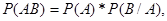 но
но 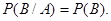
Следовательно, 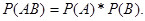
Дата добавления: 2021-11-16; просмотров: 467;











