Теорема сложения вероятностей для совместимых событий.
Теорема. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления. Т.е., если события A и B совместны, то
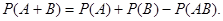
Доказательство.
Пусть испытание имеет n элементарных равновозможных исходов, из которых событию A благоприятны m исходов, событию B благоприятны k исходов, событию AB благоприятны l исходов, тогда
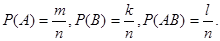
Число исходов, благоприятных сумме A+B событий A и B будет равно` 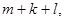 поэтому
поэтому
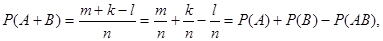
что и требовалось доказать.
В случае трех совместных событий вероятность их суммы вычисляется по формуле
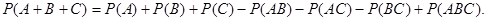
В случае же n совместных событий вероятность их суммы может вычисляться по формуле
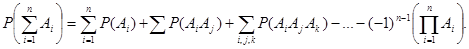
Пример 3:Три стрелка стреляют по одной цели. Найти вероятность поражения цели при одном залпе, если вероятности поражения цели соответственно равны: 0,8; 0,8; и 0,9.
Решение.
Рассмотрим события:
A – поражение цели;
B – поражение цели I - м стрелком (I =1,2,3).
Так как требуется определить вероятность поражения цели вообще, то событие A есть сумма событий 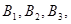 являющихся совместными и независимыми. Поэтому
являющихся совместными и независимыми. Поэтому
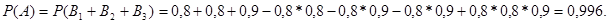
Дата добавления: 2021-11-16; просмотров: 393;











