Повторение испытаний. Формулы Бернулли.

На практике часто приходится иметь дело с сериями независимых опытов, в каждом из которых некоторое событие A может появиться или нет. При этом вероятность появления его в каждом опыте известна и она не меняется от опыта к опыту.

Примеры: появление изделий с браком в процессе производства; поступление на вход приемника серии импульсов, отраженных целью. Появление каждого импульса можно рассматривать как опыт, в результате которого импульс либо проходит на выход приемника, либо не проходит из-за помех.

В общем случае задача состоит в том, чтобы определить вероятность появления события A ровно m раз в n опытах и не появления n-m раз. Условимся считать, что вероятность события A в каждом опыте одна и та же и равна p. Следовательно, вероятность не наступления события A в каждом опыте постоянна и равна q=1-p.

Вероятность одного сложного события, состоящего в том, что в n опытах событие A наступит m раз и не наступит n-m раз равна 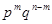( на основании теоремы умножения вероятностей независимых событий).

Так как не требуется, чтобы событие A повторилось ровно m раз в определенной последовательности, то таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по m,т.е. 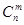. Поскольку эти сложные события несовместны и их вероятности одинаковы, то искомая вероятность будет равна

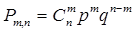, где .

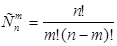Полученное выражение называют формулой Бернулли.

Пример 3:Пусть n=2: .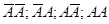

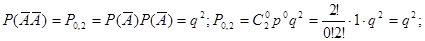
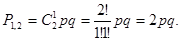
Так как 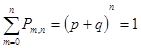, то можно определить вероятность появления события не менее m раз по следующему выражению

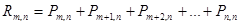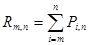, или , или .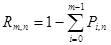

В частном случае, когда m=1 получают формулу вероятности появления события хотя бы один раз .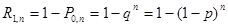

При большом числе опытов n пользоваться приведенными выше формулами неудобно, поэтому используют формулу Лапласа – Гаусса

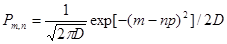, где D=n p q.