Способ непосредственного подсчета вероятностей событий.

Данный способ применяется в том случае, если опыт сводится к схеме случаев. Тогда вероятность события A определяется как отношение числа благоприятных случаев этому событию к общему числу равновозможных и несовместных исходов опыта, составляющих полную группу событий, т.е.

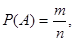
где m – число исходов, благоприятных событию;

n – число всех равновозможных и несовместных исходов опыта.

Пример 1: В ящике имеются 4 транзистора, из них 1 транзистор неисправен. Какова вероятность того, что взятый наугад транзистор будет исправным?

Решение.

A – событие того, что в результате опыта взятый наугад транзистор будет исправным.

P(A) - вероятность события A.

Так как опыт сводится к схеме случаев, число исходов конечно и m=3 , а n=4, то

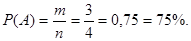
Как понимать этот результат?

Только при многократном повторении опыта в 75% случаев будет браться исправный транзистор.

Пример 2:В условиях примера 1 наугад берутся два транзистора. Требуется определить вероятность того что, что оба будут исправны.

Обозначим. B – событие соответствующее тому, что оба взятых транзистора будут исправны. P (B) - вероятность события B.

Для подсчета вероятности события обозначим транзисторы в ящике: Н – неисправный транзистор; И(1), И(2), И(3) - исправные транзисторы, и составим таблицу размещения их из 4 элементов по 2 элемента.

Таблица 1

Из таблицы легко определить числа: m=6, n=12. Откуда вероятность события B будет равна P(B)=m/n=6/12=0,5.

Вместе с этим исходы, показанные в таблице, можно толковать как размещения или как сочетания из 4 элементов по 2 т.е.

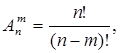
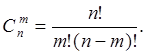
Через размещения вероятность события B можно определить следующим образом:

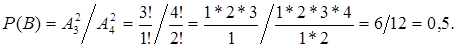
С помощью сочетаний вероятность события B определяется как

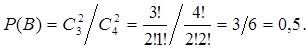
Классическим определением вероятности пользуются лишь в том случае, когда можно произвести непосредственный подсчет тех и других случаев, т.е. когда число исходов конечно. Однако на практике встречаются испытания, число возможных исходов которых бесконечно. Кроме того, часто невозможно представить исходы испытания в виде равновозможных и несовместных событий.