Б. Естественные уравнения движения

Если точка движется по известной траектории, радиус кривизны которой известен, то следует использовать в качестве системы координат оси естественного трехгранника (трехгранник Френе). Такие оси, как известно из кинематики, называются естественными осями координат 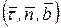. Проекции ускорения точки на естественные оси имеют вид

.

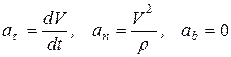Обозначая проекции сил на естественные оси через 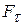, , 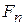, 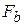получим закон движения материальной точки в проекциях на эти оси

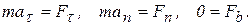(1.4)

Из этих уравнений видно, что 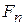> 0 и 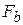= 0. Таким образом, сила, действующая на материальную точку, всегда расположена в соприкасающейся плоскости к траектории движения точки и направлена в сторону вогнутости траектории.

Пример 3. Вездеход массой 2000 кг движется по оврагу с постоянной скоростью 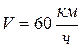. Определить давление вездехода на дно оврага, когда радиус кривизны 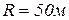. Силой сопротивления движению пренебречь.

Решение. Примем вездеход за материальную точку, тогда на нее действуют две силы: вес 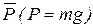и реакция грунта 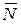(рис.1.3). Направим ось 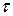по горизонтали в сторону движения, а ось n по вертикали вверх.

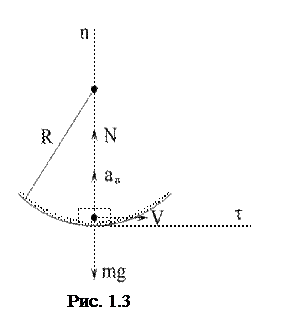Составим уравнения (1.4), учитывая, что 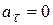поскольку .

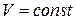Закон движения точки примет вид

, .

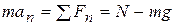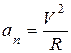Откуда

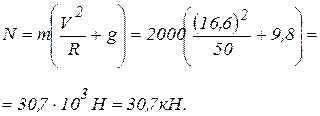
Здесь учтено, что .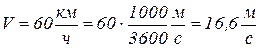

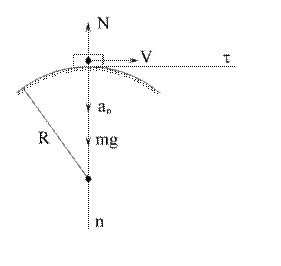Рис. 1.4

Отметим, что давление вездехода на дно оврага больше его веса 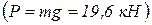. Следовательно, чтобы уменьшить давление на грунт, необходимо снизить скорость.

Если вездеход будет двигаться по холму (рис. 1.4), то направление нормальной составляющей ускорения 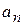будет совпадать с направлением веса вездехода .

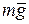Тогда

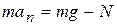, и .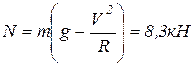

В этом случае давление вездехода на грунт будет меньше веса. Следовательно, для уменьшения давления на грунт нужно увеличить скорость.

Из примеров видно, что первая задача динамики сводится к чисто кинематическим расчетам.