Сила зависит от времени

<5 6 7 8910 11 >

Пример 6. Груз весом 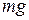начинает двигаться прямолинейно из состояния покоя вдоль гладкой горизонтальной поверхности под действием силы 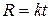, направленной вдоль оси ox. Вычислим уравнение движения груза.

Решение. Выберем начало отсчета О в начальном положении груза и направим ось oх в сторону предполагаемого движения (рис. 1.8).

Начальные условия задачи имеют вид:

при , , .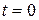

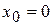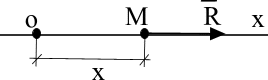
Рис.1.8

Составим закон движения груза (1.5а):

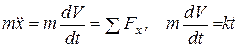Разделим переменные по известной схеме и проинтегрируем полученное уравнение с учетом начальных условий задачи

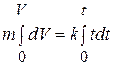, откуд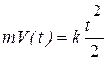а . (а)

Для определения уравнения движения тела используем подстановку 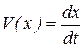, получим

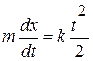Разделим переменные (помножим правую и левую части уравнения на 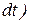и проинтегрируем полученное уравнение с учетом начальных условий

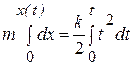Вычисляя интегралы в правой и левой части уравнения, получим уравнение движения груза

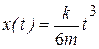4. Сила зависит от скорости

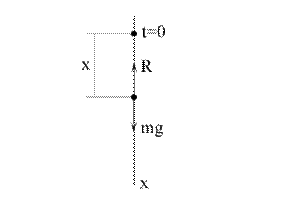Рис. 1.9

Пример 7. Точка массой m падает вертикально вниз без начальной скорости под действием силы тяжести, испытывая силу сопротивления воздуха 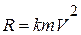, где k – положительная константа, которая зависит от плотности среды и площади проекции тела на плоскость, перпендикулярную направлению движения (рис.1.9). Найти уравнение движения точки.

Решение. Направим ось х вертикально вниз, выбрав за начало координат положение точки в нулевой момент времени, т.е. 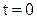(рис. 1.9). В произвольный момент времени прикладываем к точке действующие на нее силы 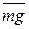и 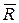. Составим дифференциальный закон движения (1.5а)

.

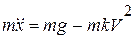Сократив на m правую и левую части уравнения и заменим 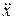на 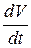, получим

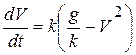. (а)

Разделим переменные, помножим на dt и разделим на 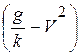правую и левую части (а). Проинтегрируем полученное выражение с учетом начальных условий:

.

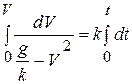Вычисляя интегралы, получим

,

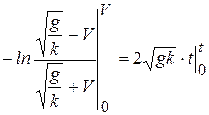откуда

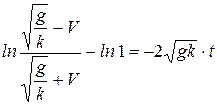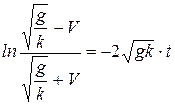или , (б)

поскольку lg1=0.

Потенцируя уравнение (б) и далее решая относительно V, имеем

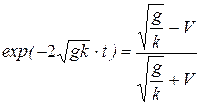, откуда 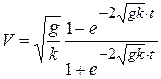. (в)

Переходя к пределу при 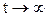, получим предельную скорость падения тела:

.

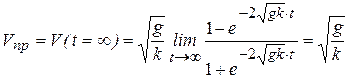Предельную скорость можно получить проще из условия максимума скорости, т.е. равенства нулю ускорения (а):

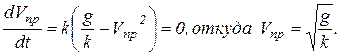
Скорость, близкая к предельной, устанавливается довольно быстро (рис. 1.10). Величина скорости зависит от значения константы k. Если не учитывать сопротивление среды (k=0), то предельного значения скорости нет: 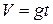пунктирная кривая на рис 1.10); при увеличении константы k , предельная скорость уменьшается.

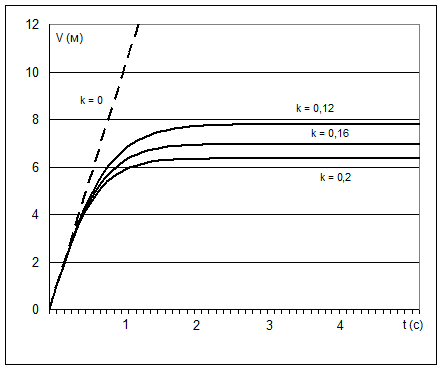
Рис.1.10

На рис 1.11 показано падение тела массой 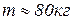с высоты без парашюта (k 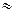0,003) – кривая В и с парашютом (k 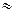0,4) – кривая С. Если начальная скорость падения тела не нулевая (например 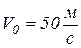), то при падении тела с парашютом (k 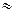0,4), скорость быстро затухает до своего критического значения – пунктирная кривая кривая D на рис.1.11.

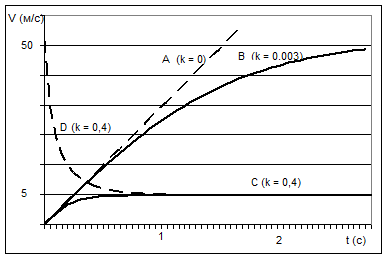
Рис.1.11

Продолжим вычисление уравнения движения падающей точки. Заметим, что правую часть выражения (в) можно представить через гиперболический тангенс (th х):

.

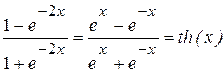Тогда выражение (в) можно записать как

.

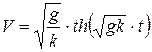Подставим вместо V ее значение 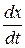, разделяя переменные и интегрируя правую и левую части, получим

,

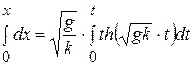или

.

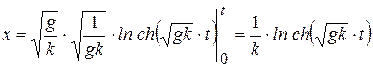Итак, уравнение движения падающей точки имеет вид

.

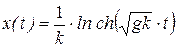Здесь ch х – гиперболический косинус.

Замечание. При вычислении интегралов полезно пользоваться таблицей интегралов.

<5 6 7 8910 11 >

Дата добавления: 2019-12-09; просмотров: 631;