Сила зависит от координаты (например, силы упругости)

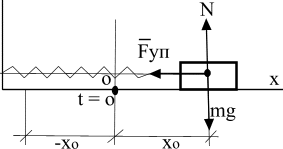Рис. 1.7

Пример 5. Груз весом mg прикреплен к правому концу пружины, левый конец которой закреплен в стене (рис.1.7). В начальный момент времени груз оттянули вдоль гладкой поверхности на величину 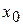и отпустили. Найти уравнение движения груза, если сила упругости пружины равна .

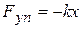Решение. Запишем начальные условия задачи:

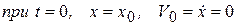. (а)

Составим дифференциальный закон движения (1.5а):

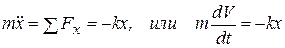. (б)

Для разделения переменных в (б), скорость нужно определить как функцию от координат, т.е. .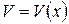

Тогда

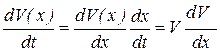. (в)

Подстановка (в) позволит исключить из дифференциального уравнения (б) время:

.

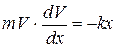Разделим переменные: умножим обе части этого уравнения на dx:

.

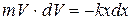Вычисляя интегралы от обеих частей уравнения с учетом начальных условий (а), получим

.

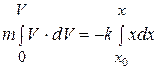Вычислим интегралы

.

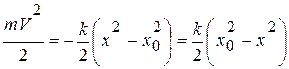Находим

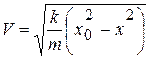. (г)

Для определения уравнения движения тела используем подстановку 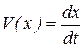, получим

.

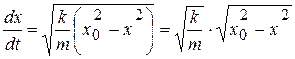Разделим переменные: умножим на dt и поделим на 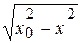правую и левую части и затем проинтегрируем полученное уравнение с учетом начальных условий (а):

.

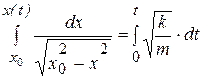Вычислим правый и левый интегралы:

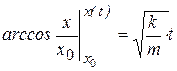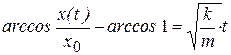или . (д)

Известно, что 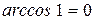, тогда уравнение движения (д) примет вид

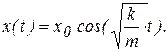
Из полученного уравнения видно, что тело будет совершать гармонические колебания с амплитудой 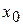(рис.1.7).