Основные виды прямолинейного движения точки

При прямолинейном движении скорость и ускорение точки все время направлены вдоль траектории точки. Совместим ось Ox с траекторией движущейся точки, тогда дифференциальное уравнение прямолинейного движения точки, согласно (1.5), имеет вид

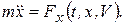(1.5а)

Начальные условия задачи задают в виде:

при .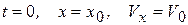

Наиболее простыми и интересными примерами прямолинейного движения материальной точки являются примеры, когда сила зависит от одного параметра.

Рассмотрим конкретные примеры на составление и интегрирование дифференциального уравнения (1.5а). Эти примеры позволят выявить некоторые особенности в решениях таких задач.

Постоянная сила

Пример 4. В результате полученного толчка тело весом mg начало скользить вниз с начальной скоростью 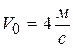по шероховатой поверхности, расположенной под углом 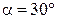к горизонту (рис. 1.6). Определить путь, пройденный телом за время 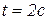, если коэффициент трения скольжения тела по поверхности равен .

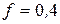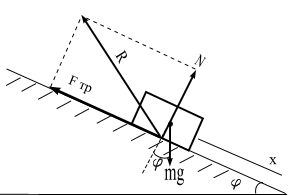Рис. 1.6

Решение. Направим ось х вдоль наклонной поверхности (рис. 1.6). Совместим начало отсчета на оси х с положением тела в начальный момент времени.

Начальная скорость 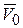направлена вдоль оси х вниз, следовательно, начальные условия задачи имеют вид

.

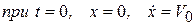Тело не является свободным. Мысленно отбросим наклонную поверхность и заменим ее действие на тело реакцией 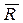. Реакция шероховатой поверхности 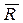имеет две составляющие: нормальную 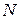и силу трения 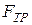( 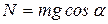и направлена перпендикулярно поверхности, сила 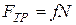направлена в сторону, противоположную предполагаемому движению).

Запишем закон движения (1.5а):

;

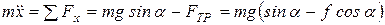и после сокращения на m , получим

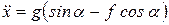. (а)

Согласно определению ускорения 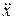= 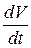, тогда (а) запишем как

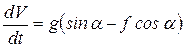. (б)

Получили линейное дифференциальное уравнение с неразделенными переменными. Для разделения переменных помножим правую и левую части уравнения (б) на dt,

.

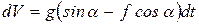Проинтегрируем правую и левую части последнего уравнения с учетом заданных начальных условий ( 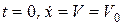). Нижние пределы интегрирования правой и левой части уравнения соответствуют значениям интегрируемых величин при t = 0, верхние пределы интегрирования – соответствуютзначениям интегрируемых величин при текущем времени t, т.е.

.

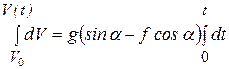Вычислим интегралы

.

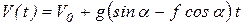Для определения уравнения движения тела используем подстановку 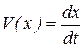, получим

.

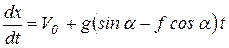Разделяя переменные

.

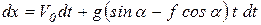Проинтегрируем полученное уравнение с учетом заданных начальных условий (t = 0, x = 0):

.

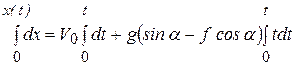Вычисляя, получим

.

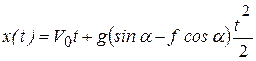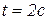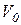Подставив заданное значение и = 4 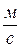, получим путь, пройденный телом за 2с:

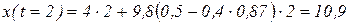м.