Движение материальной точки в пустоте

Рассмотрим движение материальной точки, на которую действует только сила тяжести (сила, имеющая постоянную величину и направление).

Выберем неподвижную систему координат так, чтобы ее начало совпадало с начальным положением точки, а ось y направим вертикально вверх. Ось x расположим в плоскости движения (рис. 1.12)

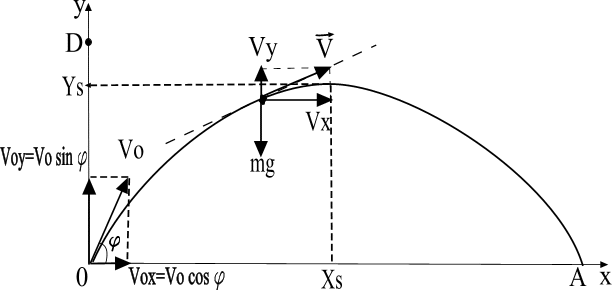
Рис 1.12

Начальная скорость точки 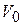образует угол 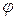с осью x. Тогда начальные условия задачи запишутся

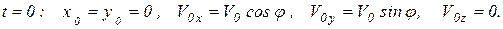(1.7)

Составим дифференциальные уравнения движения точки в проекциях на оси координат. На точку действует сила тяжести, направленная по вертикали вниз. Тогда дифференциальные уравнения движения точки в плоскости имеют вид

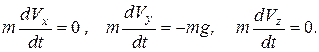(1.8)

Интегрируя первое уравнение (1.8) с учетом начальных условий (1.7), имеем

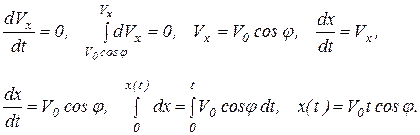
Интегрируя второе уравнение (1.8) с учетом начальных условий (1.7), имеем

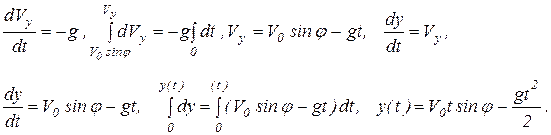
Интегрируя третье уравнение (1.8) с учетом начальных условий (1.7) имеем

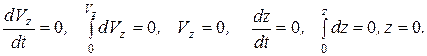
Из полученных уравнений видно, что точка движется в соприкасающейся плоскости xoy, согласно уравнениям движения

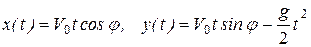. (1.9)

Проведем исследования уравнений движения точки (1.9). Исключим из них параметр t (время), получим уравнение траектории движения в явном виде

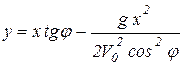, (1.10)

которое представляет собой уравнение параболы. Вершина параболы может быть определена из условия

,

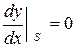т.е. ,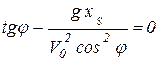

откуда

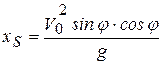. (1.11)

Дальность полета по горизонтали ОА (рис. 1.11), за счет симметричности траектории, равна

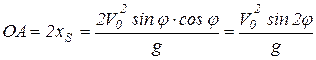. (1.12)

Из выражения (1.12) видно, что

· при углах 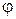и 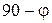тело падает в одну и ту же точку, т.к. ;

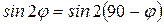· максимальная дальность полета обеспечивается при 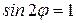, т.е. при 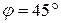, тогда дальность полета ОА (рис. 1.11) равна

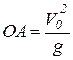. (1.13)

Подставляя значение 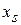в уравнение траектории (1.10), определим ординату вершины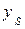

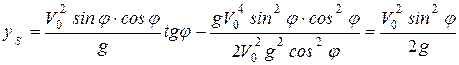. (1.14)

Из (1.14) видно: максимальная высота полета ОД (рис. 1.12) обеспечивается, когда 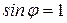, т.е. при 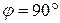, и равна

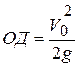. (1.14,а)

Отметим, что расстояние от начала координат до максимально возможной высоты полета зависит только от величины скорости.

Определим время 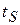, в течение которого тело поднимается вверх. Для этого достаточно решить уравнение 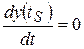, т.к. в тот момент, когда 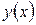достигнет наибольшего значения, проекция скорости на эту ось равна нулю, т.е.

V_y = 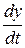=0.

Итак, используя второе уравнение из (1.9), имеем

,

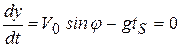откуда

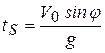. (1”)

Полное время полета 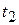определим исходя из того, что полет прекращается в тот момент, когда 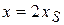. Пользуясь первым уравнением в (1.9) и (1.12), находим

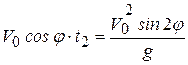, откуда 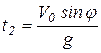. (2”)

Сравнивая выражения (1”) и (2”), видно, что при любом угле наклона броска материальной точки полное время 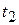полета в 2 раза больше времени 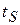подъема.