Движение снаряда в сопротивляющейся среде

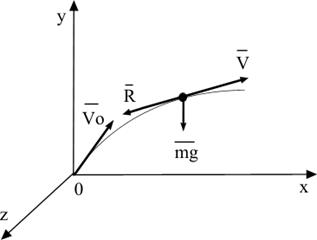Рис. 1.14

Рассмотрим задачу о полете снаряда, выброшенного из орудия с начальной скоростью 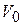под углом 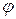к горизонту. Примем точку вылета из ствола за начало координат, ось у направим вертикально вверх, ось х будем считать горизонтальной (рис. 1.14).

Силу сопротивления воздуха примем пропорциональной скорости, т.е.

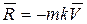. Для определенности предположим, что начальная скорость 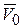располагается в плоскости хoу.

Дифференциальный закон движения точки имеет вид

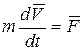. (1.16)

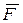Вектора и в формуле (1.16) имеют, в общем случае, по три проекци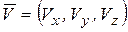и: и .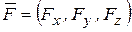

Тогда проекции векторного уравнения (1.16) на декартовы оси координат, имеют вид

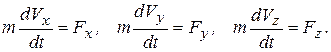(1.16,а)

На снаряд действуют две силы: сила тяжести снаряда 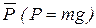, направленная вдоль оси у вниз, и сила сопротивления 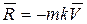, направление которой противоположно направлению скорости (рис.1.14); их равнодействующая 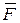, (сила, действующая на снаряд), равна их геометрической сумме этих сил:

.

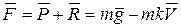Проекции силы 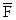на декартовы оси координат, запишутся

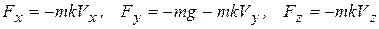. (1.17)

Тогда уравнения движения (1.16,а), учитывая (1.17), примут вид

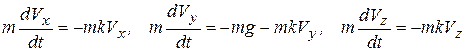. (1.18)

Запишем начальные условия задачи:

при t = 0,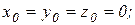

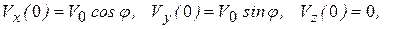(1.19)

где 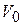- модуль начальной скорости снаряда.

После преобразования и сокращения на m, дифференциальные уравнения (1.18) примут вид

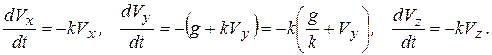(1.20)

Получили дифференциальные уравнения с неразделенными переменными.

Разделим переменные в каждом из уравнений (1.20):

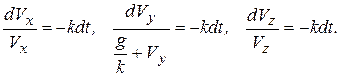
Проинтегрируем каждое из этих уравнений, с учетом начальных условий (1.19), получим

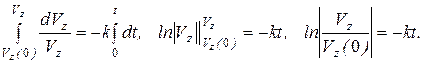
После потенцирования уравнений, имеем:

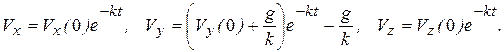
Подставляя значения начальных условий задачи (1.19), получаем

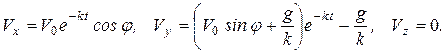(а)

Последние формулы дают возможность определить скорость снаряда в любой момент времени. Из них следует, что снаряд летит в плоскости хОу, поскольку .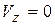

Для определения перемещений х и у вдоль координатных осей воспользуемся тем, что 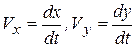. Тогда, уравнения (а) примут вид

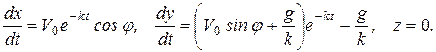(б)

Уравнения (б) снова разделились: первое из них связывает неизвестную функцию 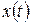, а второе – функцию .

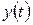Разделяя переменные в уравнениях (б) и интегрируя с учетом начальных условий (1.19), находим:

;

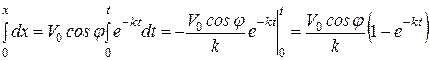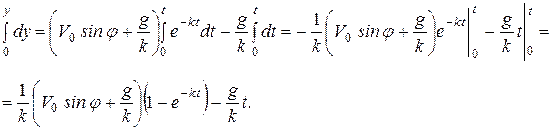
Получили уравнения движения точки в плоскости в виде

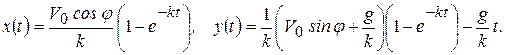(1.21)

Формулы (1.21) дают возможность определить положение снаряда в любой момент времени.

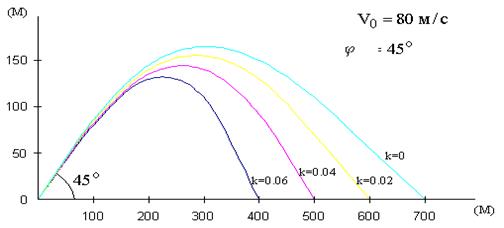На рис 1.15 представлены траектории движения снаряда с различными коэффициентами k, т.е. в средах различной плотности.

Рис.1.15

Путем предельного перехода при 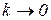, получим уравнения движения снаряда под действием одной силы тяжести. Обозначим координаты в этом случае 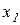и 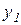. При вычислении пределов используется формула разложения в ряд экспоненты

.

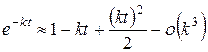Для х(t) из (1.21) получаем

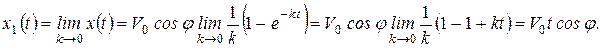
Прежде чем переходить к пределу в из (1.21), преобразуем выражение: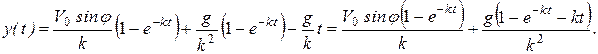

Тогда

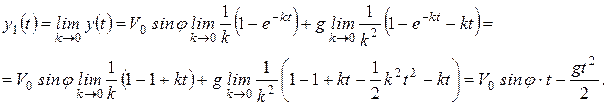
Получили уравнения движения точки под действием одной силы тяжести, которые соответствуют полученным раньше (1.9).

Отметим, что траектории движения тела (1.21) не являются в точности параболами. В действительности траектории еще сложнее, поскольку снаряд при движении испытывает сопротивление воздуха; ускорение свободного падения g зависит от высоты над поверхностью Земли; определенные поправки в процесс попадания снаряда в цель вносит вращение Земли.

При решении реальных задач всегда пренебрегают теми или иными факторами. Так, если при небольшой начальной скорости тела ( 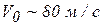) роль сопротивления воздуха невелика, то при больших 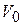, например при 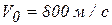, сопротивлением воздуха пренебрегать нельзя; сопротивление воздуха уменьшает дальность полета снаряда от получающегося по формуле (1.11) значения 61 км до 22,2 км по формулам (1.21).