Связь угловых характеристик вращающегося твердого тела с линейными кинематическими характеристиками вращающегося тела

Как уже отмечалось, траекторией любой точки М вращающегося тела является дуга окружности, лежащая в плоскости перпендикулярной оси вращения. Радиус этой окружности равен расстоянию от точки до оси. Рассмотрим траекторию движения некоторой точки М тела, вращающегося вокруг оси, перпендикулярной плоскости рисунка и проходящей через центр окружности (рис. 5.3).

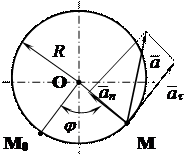Рис. 5.3

Если отсчитывать дуговую координату s точки М от ее начального положе­ния М₀ в направлении возрастания угла j, то закон движения точки М по дуге окружности будет иметь вид 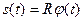. В этом случае алгебраическое значение скорости определяется по формуле:

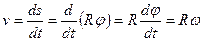. (5.6)

Найдем ускорение точки М:

.

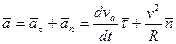Продифференцировав (5.6) по времени, определим алгебраическую величину касательного ускорения:

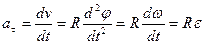. (5.7)

Нормальное ускорение получим, подставляя (5.6) в выражение для нормального ускорения:

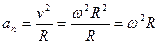. (5.8)

Следовательно, для вектора ускорения имеем:

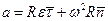. (5.9)

Для модуля ускорения точки М имеем формулу:

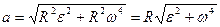. (5.10)

Из выражений (5.6) и (5.10) следует, что линейные кинематические характеристики точек зависят от угловых характеристик вращающегося твердого тела, а коэффициентом пропорциональности является радиус вращения.