Сложное движение точки

До сих пор движение точки рассматривалось по отношению к неподвижной системе координат, но в ряде случаев целесообразно изучать движение точки одновременно в двух системах отсчёта, из которых одна является неподвижной, а другая - подвижной, совершающей определённым образом движение относительно первой. Движение точки, в этом случае, называют сложным.

На рис. 5.4 изображены две системы координат: неподвижная Oxyz и подвижная O₁x₁y₁z₁. Движение, совершаемое точкой М по отношению к подвижной системе координат O₁x₁y₁z₁называется относительным движением. Движение подвижной системы отсчёта O₁x₁y₁z₁ и всех точек пространства с ней связанных по отношению к неподвижной системе Oxyzназывается переносным движением. Движение точки Мотносительно неподвижной системы координат Oxyz называется абсолютным.

Скорость точки М по отношению к неподвижной системе координат называется абсолютной скоростью точки.

Скорость точки М по отношению к подвижной системе координат называется относительной скоростью точки.

Переносной скоростью точки М называется скорость подвижной системы относительно неподвижной, в которой в данный момент времени находится движущаяся точка М.

Теорема о скорости точки в сложном движении.

Вектор абсолютной скорости точки в данный момент времени равен геометрической сумме векторов относительной и переносной скоростей в тот же момент времени.

Доказательство.

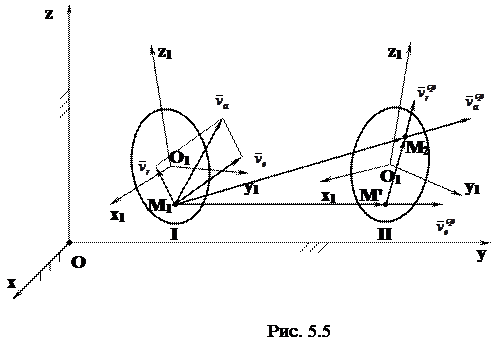
Пусть тело S, неизменно связанная с ним подвижная система отсчёта O₁x₁y₁z₁ и точка М₁ занимают в момент времени t₁ положение I (рис. 5.5) относительно неподвижной системы Oxyz. Пусть в момент времени t₂=t₁+Dt тело S и система O₁x₁y₁z₁ займут положение II, а точка М₁ перейдёт в точку М₂. Буквой М' обозначим положение той точки тела S, в которую переместится за время Dt его точка, совпадающая в момент t₁ с М₁.

Вектор 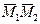изображает абсолютное перемещение точки, вектор 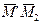относительное перемещение, вектор 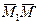переносное перемещение точки за время Dt. Для этих векторов справедливо следующее равенство

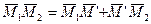. (5.11)

Разделив (5.11) почленно на Dt, получим

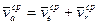, (5.12)

где 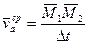- средняя абсолютная скорость;

- средняя переносная скорость;

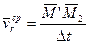- средняя относительная скорость.

Переходя в (5.12) к пределу при Dt стремящемся к нулю, получим

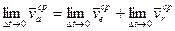, или 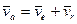(5.13)

Теорема доказана.

Согласно доказанной теореме вектор абсолютной скорости 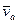изображается диагональю параллелограмма, построенного на векторах переносной 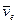и относительной 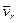скоростей. Модуль 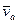вычисляется по теореме косинусов

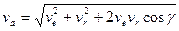, (5.14)

где g - угол между векторами переносной и относительной скоростей.