Понятие о плоскопараллельном движении твердого тела

Движение твердого тела называется плоскопараллельным, если все точки тела перемещаются в плоскостях, параллельных некоторой фиксированной плоскости (основной плоскости).

Пусть некоторое тело V совершает плоское движение, p - основная плос­кость (рис. 5.4). Из определения плоскопараллельного движения и свойств аб­солютно твердого тела следует, что любой отрезок прямой АВ, перпендикуляр­ный плоскости p, будет совершать поступательное движение. То есть траекто­рии, скорости и ускорения всех точек отрезка АВ будут одинаковы. Таким об­разом, движение каждой точки сечения s параллельного плоскости p, опреде­ляет собой движение всех точек тела V, лежащих на отрезке перпендикулярном сечению в данной точке.

Примерами плоскопараллельного движения являются: качение колеса по прямолинейному отрезку, так как все его точки перемещаются в плоскостях, параллельных плоскости, перпендикулярной оси колеса; частным случаем та­кого движения является вращение твердого тела вокруг неподвижной оси, в са­мом деле, все точки вращающегося тела движутся в плоскостях параллельных некоторой перпендикулярной оси вращения неподвижной плоскости.

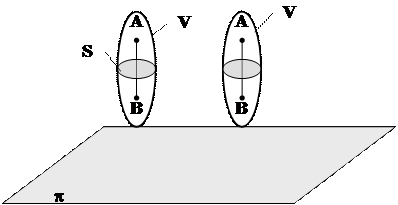Рис. 5.4

Теорема о возможности представления плоскопараллельного движения в виде совокупности двух движений: поступательного и вращательного.

Пусть некоторое тело совершает плоскопараллельное движение. Рассмотрим некоторое сечение этого тела параллельное основной плоскости.

Произвольно выбранную точку сечения или плоскости, которой принадлежит сечение и которая неизменно связана с сечением, называют полюсом.

Теорема. Всякое перемещение плоской фигуры в её плоскости может быть представлено в виде совокупности двух движений: поступательного и вращательного.

Доказательство.

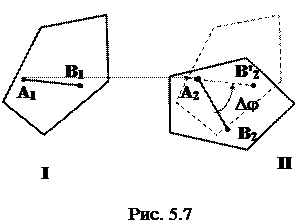Пусть плоская фигура за некоторый промежуток времени Dt переместилась из положения I в положение II (рис. 5.7). Положение произвольно выбранного отрезка неизменно связанного с фигурой, определяет положение всей фигуры в любой момент времени. Выберем две произвольные точки фигуры А₁ и В₁ и примем точку А₁ за полюс. Отрезок А₁В₁ через промежуток времени Dt займёт положение А₂В₂. Поступательным перемещением фигуры совместим точки А₁ и А₂. Точка В₁ при этом займёт положение В'₂, а сама фигура перейдёт в положение, отмеченное пунктиром. Поступательное перемещение фигуры определится вектором 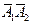, и отрезок А₁В₁ будет параллелен отрезку А₂В'₂. Если теперь повернуть фигуру вокруг полюса А₂ на угол Dj=ÐВ'₂А₂ В₂, то отрезок А₂В'₂ займёт положение А₂В₂, а сама фигура - положение II, что и требовалось доказать.

Теорема рассматривает не реальное, а возможное движение точки.

Следствие из теоремы: Угловая скорость плоской фигуры не зависит от выбора полюса.