Вращение твердого тела вокруг неподвижной оси

Вращательным движением твердого тела называется движение, при котором две его точки А и В остаются неподвижными. Так как тело абсолютно твердое, то вместе с точками А и В будут неподвижны все точки, лежащие на прямой АВ. Эта прямая называется осью вращения (рис. 5.2). Все точки тела при вращательном движении описывают дуги окружностей с центрами в основаниях перпендикуляров, опущенных из этих точек на ось вращения.

Проведем через ось вращения две полуплоскости, одну из которых зафиксируем, а другую свяжем с телом. Двугранный угол j, угол поворота, между этими полуплоскостями будет однозначно определять положение тела. Задавая значение угла j в каждый момент времени t, можно тем самым определить положение тела для любого t. Уравнение

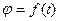(5.3)

носит название закона вращательного движения тела. Функция (5.3) предполагается дважды дифференцируемой.

Главными кинематическими характеристиками вращательного движения тела будут угловая скорость w (с^-1) и угловое ускорение e (с^-2).

Пусть за некоторый промежуток времени 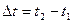угол j получит приращение 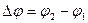. Величина 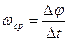называется средней угловой скоростью тела. Предел, к которому стремится средняя угловая скорость при Dt®0, называется угловой скоростью тела в данный момент времени t.

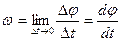. (5.4)

Если тело совершает вращательное движение по произвольному закону, то угловая скорость является функцией времени: .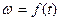

Пусть за некоторый промежуток времени 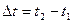угловая скорость получила приращение 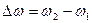. Величина 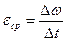называется средним угловым ускорением. Предел, к которому стремится среднее ускорение при Dt® 0, называется угловым ускорением в данный момент времени t.

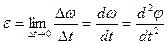. (5.5)