Мгновенный центр скоростей

Мгновенным центром скоростей называется такая точка плоской фигуры (или неизменно связанной с этой фигурой плоскости), скорость которой в данный момент времени равна нулю.

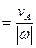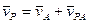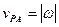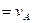Пусть фигура S (рис. 5.9) совершает плоскопараллельное движение, причем угловая скорость этого движения не равна нулю. Примем произвольную точку А фигуры S за полюс. Повернём вектор скорости точки А вокруг его начала в сторону вращения на угол p/2 и отложим в полученном направлении отрезок АР . Действительно из (5.15) имеем , причем АР , а направление вектора 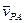противоположно 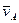. Следовательно, 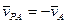и .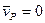

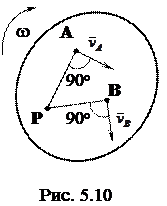Приняв за полюс мгновенный центр скоростей, получим выражение для скорости произвольной точки А в виде: 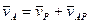, но 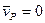, тогда 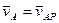, 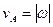АР, то есть скорости точек плоской фигуры в данный момент времени распределены таким образом, как если бы эта фигура вращалась вокруг мгновенного центра скоростей с угловой скоростью w.

Если А и В - произвольные точки тела, Р - мгновенный центр скоростей (рис. 5.10), то поскольку 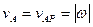АР, 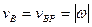ВР, получим

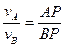. (5.16)

Таким образом, скорости точек плоской фигуры прямо пропорциональны их расстояниям до мгновенного центра скоростей.

Лекция 6

Динамика

Динамика – раздел теоретической механики, изучающий движение матери­альных объектов и причины его вызывающие.

Движение тела считается известным, если известно движение каждой его точки; поэтому изучение динамики начинается с изучения движения матери­альной точки. Под материальной точкой понимают тело, размеры которого та­ковы, что различием в перемещениях отдельных его частиц можно пренебречь. Материальную точку можно рассматривать как геометрическую точку, имею­щую конечную массу.