Косвенные методы построения функции принадлежности
Наиболее показательным для этой группы методов является метод попарных сравнений, разработанный Т. Саати, суть которого состоит в следующем.
Пусть х1, х2, ..., xn являются элементами базового множества Х и носителями нечеткого множества А:хiÎ Х, S{хi}, а w1, w2,...,wn - соответственно их веса (интенсивности) или степень принадлежности mА(хi). Попарное сравнение весов wi, wj или принадлежности хi и хj (i, j =1, ...,n) к понятию А можно зафиксировать в виде матрицы попарных сравнений (или матрицы суждений) W º [aij], где aij – результат попарного сравнения xi и xj т.е. wi /wj .
 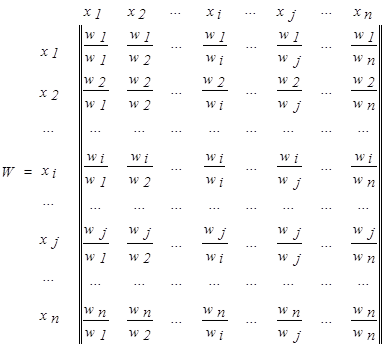
| (3.21) |
Полученная матрица является квадратной, симметричной, т.е. количество строк и столбцов равно n и элементы матрицы аij =1/ аji. Такая матрица имеет собственные векторы и собственные значения[2].
Если w1, w2,...,wn неизвестны заранее, то попарное сравнение элементов хi и хj, производится с использованием субъективных суждений, численно оцениваемых по шкале (табл.3.3), а затем решается проблема нахождения wi, т.е. mА(хi).
Приведенная шкала (табл.3.3) дает возможность улавливать разницу в чувствах и суждениях экспертов, проводивших сравнения. При этом эксперт должен быть уверенным во всех градациях суждений одновременно. Психологами установлено, что для лучшей согласованности и точности индивидууму не следует одновременно сравнивать более 7 ± 2 объектов. Это определило выбор шкалы в пределах от 1 до 9 (0 можно не принимать во внимание).
Таблица 3.3. Шкала относительной важности
| Интенсивность относительной важности (принадлежности) | Качественная оценка или определение | Пояснение |
| Несравнимость | Нет смысла сравнивать элементы | |
| Одинаковая важность (принадлежность) | Элементы равны по важности (принадлежности) | |
| Слабое превосходство одного над другим | Существуют некоторые данные или суждения, о предпочтении важности (принадлежности) одного элемента в сравнении с другим | |
| Заметное превосходство | Существуют некоторые доказательства, например логические, которые могут показать, что один из элементов более важен (имеет более отчетливую принадлежность) | |
| Очевидное превосходство | Существуют убедительные доказательства большей важности (принадлежности) одного элемента по сравнению с другим | |
| Важность (принадлежность) несравнима | Очевидно превосходство по важности (принадлежности) одного элемента по сравнению с другим | |
| 2, , 4, 6, 8 | Промежуточные решения между двумя соседними суждениями | Применяются в компромиссных случаях |
| Обратные величины приведенных выше чисел | Если оценка аij имеет ненулевое значение при сравнении хi и хj, то аji =1/ аij |
Таким образом, элементы матрицы W аij = wi / wj принимают значения, данные экспертом на основании приведенной шкалы. Обработка результатов экспертного заключения, выраженных в виде матрицы W, осуществляется следующим образом:
1) вычисляются суммы каждого столбца матрицы W как
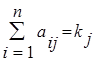 ; ;
| (3.22) |
2) на основании kj образуются элементы собственного вектора матрицы W, а именно,
w = (w1, w2,...,wn), где
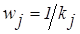 . .
| (3.23) |
Справедливость (3.23) доказывается следующим образом:
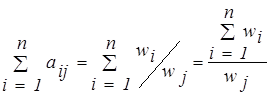 , ,
|
с учетом того, что 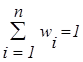 , получим
, получим
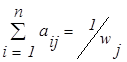 ; ;
| (3.24) |
приравнивая (3.22) и (3.24), будем иметь (3.23);
3) оценивается точность определения собственного вектора w=(w1 w2,...,wn).
Для этого подставляются вычисленные значения вектора w в выражение Ww.
Если принятые в матрице отношения аij точны, то получается Ww = nw, где n – собственное значение матрицы W. В общем случае эмпирический вектор w = (w1, w2,...,wn)Т должен соответствовать решению общей задачи с симметричными суждениями, сводящейся к решению уравнения матрицы W:
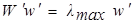 , ,
| (3.25) |
где lmax - наибольшее соответственное значение матрицы W.
В связи с этим полученный в результате перемножения Ww вектор делят поэлементно на вектор w и получают вектор l, в котором i-й элемент есть значение lmax , соответствующее элементу wi вектора w.
Оценку точности определения собственного вектора w (степень нарушения численной, т.е. 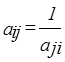 и транзитивной, т.е. аkj. = аik , cогласованности суждений) можно осуществлять по усредненному значению `
и транзитивной, т.е. аkj. = аik , cогласованности суждений) можно осуществлять по усредненному значению ` 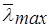 :
:
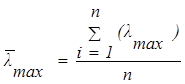 , ,
| (3.26) |
сравнивая это значение с n. Тогда точность решения будет равна:
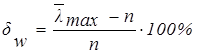 . .
| (3.27) |
Как правило, начальная оценка вектора w по предложенному методу в большинстве случаев получается достаточно хорошей и при отсутствии повышенных требований к точности определения вектора w (т.е. mА(хi)) дальнейшее его уточнение может не проводиться. В противном случае экспертам необходимо вновь исследовать задачу, проверить свои суждения и просчеты повторить.
Более определенный подход к оценке вектора w предложен Т. Саати. Вводится индекс согласованности
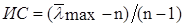 . .
| (3.28) |
Исходя из размера матрицы W устанавливается значение случайной согласованности СС (табл.3.2).
Таблица 3.4.Случайные согласованности
| Размер матрицы n | ||||||||||
| Значение случайной согласованности, СС | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
Если разделить ИС на соответствующее значение СС, то получится отношение согласованности - ОС:
| ОС = ИС/ СС. | (3.29) |
Величина ОС должна быть не более 10 %, т.е. ОС < 10 %. Лишь в случаях, требующих приблизительной (качественной) оценки W допускается ОС< 20 %.
Следует отметить, что вектор соответствует субнормальной функции принадлежности, поэтому в завершении W требуется процедура нормализации mА(хi).
Пример 3.7. Для девяти предметов х1, х2, ... ,x9 (хiÎХ) необходимо определить степень принадлежности понятию (нечеткому множеству А) “полезный”. В результате опроса эксперта получена матрица попарных сравнений
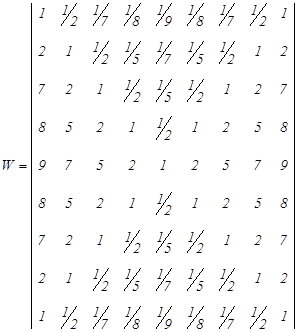 ,
,
1) просуммируем элементы столбцов матрицы и по (3.23) определим собственный вектор w с элементами:
w1= 0,02; w2= 0,04; w3= 0,08; w4=0,18; w5=0,34; w6 =0,18; w7= 0,08; w8= 0,04; w9 = 0,02; т.е.;
w = (0,02; 0,04; 0,08; 0,18; 0,34; 0,18; 0,08; 0,04; 0,02);
2) оценим точность определения элементов вектора w; при этом после умножения матрицы W на вектор w получим вектор чисел:
(0,18; 0,36; 0,85;1,57;2,96;1,57;0,85;0,36;0,18); поделив полученный вектор поэлементно на вектор w, получим вектор l = (9;9;10,6;8,7;8,7; 8,7;10,6;9;9), в котором i - элемент есть значение lmax, соответствующее элементу wi вектора w
| lmax = 9,25, | ИС = 0,25/8 = 0,031, |
| dw = 3 %, | ОС = 0,031/1,45 » 0,02 |
| или 2 %. |
Такая точность определения элементов вектора w достаточна.
Таким образом, с точностью 2 % получаем
mА(х1) = 0,02; mА(х2= 0,04; mА(х3) = 0,08; mА(х4) = 0,18; mА(х5) = 0,34;
mА(х6) = 0,18; mА(х7) = 0,08; mА(х8) = 0,04; mА(х9) = 0,02
или в нормализованном виде
А={<0,06/ х1>,< 0,12/ х2 >, < 0,24/ х3 >, < 0,53/ х4 >, < 1/ х5>, < 0,53/ х6>,
< 0,24/ х7>, < 0,12/ х8 >, < 0,06/ х9>}.
Существует аналогичный метод определения функции принадлежности по матрице бинарных отношений: А= ((аij))=((wi/wj)). Принципиальное отличие заключается в том, что вместо поиска собственного значения вектора матрицы используется метод наименьших квадратов, т.е. искомые значения mА(хi) получаются путем решения оптимизационной задачи:
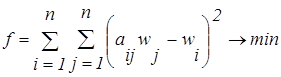
| (3.30) |
при условии 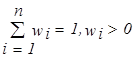 . Следует отметить, что оба указанных косвенных метода близки по своей точности.
. Следует отметить, что оба указанных косвенных метода близки по своей точности.
При участии группы экспертов после обсуждения и консенсуса можно объединить разные суждения, удовлетворив условия симметричности матрицы попарных сравнений (матрицы бинарных отношений). Независимо от правила, которое применяется для объединения суждений и соответствующих им обратных величин, они должны совпадать с тем, что получилось бы, если объединить обратные величины этих суждений. Для выполнения этого существует, например, такой способ: перемножаются собственные численные значения и извлекается корень k - степени, где k - число экспертов, т.е. определяется геометрическое среднее.
В условиях отсутствия четкой грани между допустимым и недопустимым в пространстве неуправляемых параметров и между идеальным и неудовлетворительным состоянием в пространстве критериев построение функции принадлежности осуществляется на основе интервальных оценок.
Рассмотрим ситуацию, когда известна связь между некоторым параметром z и критерием выбора h. Эксперту, известно, что критерий h зависит от z (параметр среды функционирования анализируемых объектов). Существует теория возможностей, основанная на предположении, что эксперт может указать интервал [h*, h0] (h* и h0 - граничные значения), которой соответствует пожеланию - выбрать «хороший» объект имеет следующую интерпретацию: объект - а, параметр ha- результат измерения значения характеристики h для объекта а, h* это граница «идеальной» области.
Если ha ≥ h*, то объект следует признать «идеально» соответствующим понятию хороший. Возможность такого утверждения π(Q) равна 1, где Q - субъективное событие, заключающееся в том, что объект с точки зрения экспертов находиться в состоянии «хороший».
Если ha £ h0, то возможность того, что объект а - «хороший»: π(Q)=0. При ha < h* и ha > h0 возможность признать объект «идеальным» равна 0< π(Q) < 1. Графически это интерпритируется, как представлено на рис.3.5.
Ощущение эксперта позволяет использовать рабочую гипотезу, заключающуюся в том, что с приближением значения ha к h* возможность признания объекта а «хорошим» линейно возрастает.

Рис.3.5. Возможные области объекта
Если эксперт подтверждает указанную логику размышления, то воспользуемся формулой:

| 0, | если ha £ h0 | (3.31) | |
| π(Q)= | 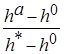 , ,
| если h0 < ha <h* | ||
| 1, | если ha ≥ h* |
Графически это это можно изобразить, как показано на рис.3.6.

Рис.3.6. Линейная модель возможного состояния объекта
До настоящего момента предполагалось, что h представляет собой критерий типа «выигрыш», т.е. h* > h0, во всем диапазоне «цели» z. Если h0>h*, то для расчета возможностей используется критерий типа «штраф», в линейном случае для этого в формулу (3.31) вносятся соответствующие изменения.
Представления эксперта могут не позволить применять линейную модель. В это случае используются модели, представленные на рис.3.7.
Задачу выбора модели можно решить приближенно, предлагая эксперту в единичном интервале [0;1] указать место некоторой средней величины h. Наличие трех значений фукнции m(h), указанное экспертом, 0 и 1 позволяет полностью востановить функцию в интервале [h0; h*].

Рис.3.7. Нелинейная модель возможного состояния объекта
В задаче выбора объекта экперты могут считать, что границы h0 и h* при фиксированном значении параметра z имеют значения, приведенные на рис.3.8.


Рис.3.8. Функции уровневых ограничений
Апроксимируя данные получаем аналитические выражения двух функций h*(z) и h0(z), которые называются уровневыми ограничениями.
Эти функции путем экспертного опроса можно построить таким образом, чтобы охватить весь диаапазон реального изменения параметра z. Для получения полного представления об объекте а надо провести ряд экспериментов по поределению оценки ha при различных значениях z. В результате апроксимации имеем функцию ha(z).

Рис.3.9. Функция распределения возможности
Полученная фунций π(z) называется распределением возможности и представляет собой нечёткое ограничение на значение парамтра z, т.е. возможность применения объекта плавно меняется о идеальной пригодности до его недопустимости использования.
На практике возможны различные мнения экспертов о храктере уровневых ограничений:
а) согласованные функции.
Могут возникнуть в случае достаточно ясных представлений экспертов о предметной среде.

Рис.3.10. Согласованные функции
б) расходящиеся функции.
 Могут свидетельствовать о том, что эксперту недостаточно известно поведение объекта при больших значениях параметра z и/или большие значения z маловероятны.
Могут свидетельствовать о том, что эксперту недостаточно известно поведение объекта при больших значениях параметра z и/или большие значения z маловероятны.
Рис.3.11. Расходящиеся функции
в) сходящиеся функции.
Могут возникнуть в задаче оценки объектов, имеющих экстремальный характер функционирования при больших значениях z.

Рис.3.12. Сходящиеся функции
г) функции с конечными разрывами отражают либо качественные скачки в процессах физического мира или влияние законов и нормативных актов на мнения экспертов.

|
| Рис.3.13. Функции с конечными разрывами |
д) соединяющиеся и разъединяющиеся функции.
Могут возникнуть в случае, когда в некоторых областях значение параметра z эксперты имеют четкое мнение.

Рис.3.14. Соединяющиеся и разъединяющиеся функции
е) несогласованные функции представляют собой случаи, когда предварительно найти трудно мотивацию такого мнения эксперта. Подобная модель, вероятно, является следствием ошибки.

Рис.3.15. Несогласованные функции
ж) унимодальные функции должны быть использованы экспертами, если известно, что все объекты имеют унимодальную характеристику ha = f(z).

Рис.3.16. Унимодальные функции
з) пересекающиеся функции соответствуют реверсивной задаче, когда при определении параметра z меняется характер использования критерия.

Рис.3.17. Пересекающиеся функции
Субнормальное распределение возможностей будет иметь место в том случае, когда во всем рассмотренном диапазоне значений параметра z объект a не имеет ha ≥ h*.
Пример 3.8.Необходимо найти распределение возможностей для приведенной в табл. 3.5 характеристики объекта ha и варианта уровневых ограничений.
Таблица 3.5. Расчетные данные для примера 3.8
| Значение параметра z | Объект ha | Ограничение | |
| h* | h0 | ||
Рассматриваемая модель - линейная.
1. z = 3; т.к. h a < h0 Þ π(z) = 0;
2. z = 6; т.к. h0<h a<h*15 Þ π(z) = 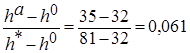 ;
;
3. z = 9; т.к. h0<h a<h*15 Þ π(z) = 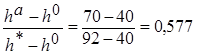 ;
;
4. z = 12; т.к. h0<h a<h*15 Þ π(z) = 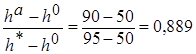 ;
;
5. z = 15; т.к. h a > h* Þ π(z) = 1;
Построим функцию принадлежности.

Рис.3.18. Функция принадлежности линейной модели
Дата добавления: 2021-10-28; просмотров: 514;











