Формирование базы правил систем нечеткого вывода.

База правил {R_i}^k_i=1 системы нечеткого вывода предназначена для формального представления эмпирических знаний экспертов в той или иной проблемной области. База правил системы нечеткого вывода представляет собой конечную совокупность нечетких правил, согласованную относительно используемых в них лингвистических переменных. Наиболее часто база правил представляется в виде структурированного текста:

{Ri}ki=1=		R1: ЕСЛИ А1 ТО B1	( 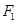)	(4.44)
R2: ЕСЛИ А2 ТО B2	( )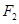
R3: ЕСЛИ А3 ТО B3	( )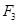
…
RN: ЕСЛИ АN ТО BN	( )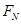

где 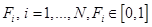- коэффициенты определенности или весовые коэффициенты соответствующих правил. В случае, когда весовые коэффициенты отсутствуют, удобно принять, что они равны 1.

В системах нечеткого вывода лингвистические переменные, которые используются в нечетких высказываниях подусловий нечетких правил, часто называют входными лингвистическими переменными. А переменные, которые используются в нечетких высказываниях подзаключений правил нечетких продукций, часто называют выходными лингвистическими переменными.

Таким образом, при формировании базы правил нечетких продукций необходимо определить:

1. Множество правил нечеткой продукции {R_i}^k_i=1 в форме (4.44)

2. Множество выходных лингвистических переменных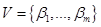

3. Множество выходных лингвистических переменных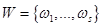

Для базы правил справедливы следующие свойства:

- непрерывность;

- непротиворечивость;

- полнота.

Для того чтобы определить непрерывность {R_i}^k_i=1, используются сле­дующие понятия:

- упорядоченная совокупность нечетких множеств;

- прилегающие нечеткие множества.

Совокупность нечетких множеств {A_i} называется упорядоченной,если для них задано отношение порядка, например:

“<”: A₁<A₂<…<A_i-1<A_i<A_i+1<…

Если {A_i} упорядочена, тогда множества A_i-1 и A_i, A_i и A_i+1 называ­ются прилегающими. Здесь предполагается, что эти нечеткие множества являются перекрывающимися.

База правил {R_i}^k_i=1 называется непрерывной, если для правил

R_k : если х₁ = A_1k и х₂ = A_2k, тогда y = B_k и k' ¹ k имеем:

- А_1k = А_1k' 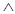A_2k и A_2k' являются прилегающими;

- А_2k ⁼ А_2k' 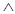A_1k и A_1k' являются прилегающими;

- B_k и B_k' являются прилегающими.

Непротиворечивость базы правил демонстрируем на примерах 4.10 и 4.11.

Пример 4.10. Нечеткое управление роботом.

…

или

R_k: если препятствие впереди, то двигайся влево,

{R_i}ⁿ_i=1 = или

R_k+l: если препятствие впереди, то двигайся вправо,

или

…

База правил {R_i}ⁿ_i=1 противоречива.

Пример 4.11. Нечеткая система (рис.4.4)

R₁: если x_l = А или х₂ = Е, тогда у = Н;

{R_i}³_i=1 = R₂: если x_l = С или х₂ = F, тогда у = I;

R₃: если x_l = В или х₂ = D, тогда у = G .

В терминах управления правила, которые содержат два условия и один вывод, представляют собой систему с двумя входами х₁, х₂ и одним вы­ходом у, В этом случае алгоритм функционирования нечеткой системы может быть задан в матричной форме, как показано на рис.4.4.

x1 x2	A	B	C
D		G	y
E	H
F		I

Рис.4.4. Пример задания функционирования нечеткой системы

Представленная база правил непротиворечива. Пусть теперь база пра­вил имеет вид:

x1 x2	A	B	C
D		G
E	H		H
F		I

Рис.4.5. Противоречивость базы правил

В этом случае база правил противоречива, т.к. она приводит к двусмысленности выводов, как показано в примере 4.10. Этот феномен не так легко может быть идентифицирован, в общем случае, при наличии сложной базы правил.

Полнота {R_i}^k_i=1 используется как мера, указывающая на полноту знаний, которые содержаться в базе правил. Неполная база правил имеет так называемые «пустые места» для определенных ситуаций (на семантиче­ском уровне), т.е. не определены связи между входами и выходами. Это не означает, что результат вывода из правила не существует из-за неполноты базы правил, а этот эффект обусловлен свойствами нечетких множеств, которые используются в условиях правил.

В качестве меры полноты используется критерий:

,

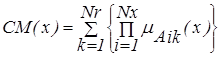(4.45)

где х - физическая переменная входных данных (условий); N_x - число условий в правиле; N_r - число правил в базе правил. Например, при N_x=1, N_r=1, что соответствует наличию одного условия (N_x = 1) базе правил, содержащей одно правило (N_r =1), получим:

.

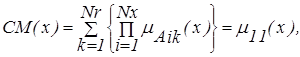
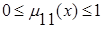Если m₁₁(х)= 0 , что соответствует пустому месту, получим СМ(х) = 0 . Численные значения, которые принимает критерий СМ(х), позволяют классифицировать базы правил по полноте знаний:

• СМ(х) = 0 - «неполная» база правил;

• 0 < СМ(х)<1 - база правил «незначительно полная»;

• СМ(х) = 1 - база правил «точно полная»;

• СМ(х)>1 - база правил «сверхполная (избыточная)».

Таким образом, при разработке алгоритмов нечетких систем управле­ния в виде базы правил обязательным этапом анализа алгоритма является проверка соответствующей базы правил на непрерывность, непротиворе­чивость и полноту и далее приступают к компьютерной реализации алго­ритма управления.

Фаззификация

В контексте нечеткой логики под фаззификацией понимается не только отдельный этап нечеткого вывода, но и собственно процесс или процедура нахождения значений функции принадлежности нечетких множеств (термов) на основе обычных (не нечетких) исходных данных. Фаззификацию еще называют введением нечеткости.

Целью этапа фаззификации является установление соответствия между конкретным, обычно численным, значением отдельной входной переменной системы нечеткого вывода и значением функции принадлежности соответствующего ей терма входной лингвистической переменной. После завершения этого этапа для всех входных переменных должны быть определены конкретные значения функций принадлежности по каждому из лингвистических термов, которые используются в подусловиях базы правил системы нечеткого вывода.

Формально процедура фаззификации выполняется следующим образом. До начала этого этапа предполагаются известными конкретные значения всех входных переменных системы нечеткого вывода, т.е. множество значений 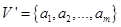. В общем случае каждо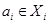е , где 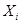- область определения лингвистической переменной .

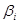Далее рассматривается каждое из подусловий вида 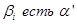правил системы нечеткого вывода, где 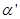- некоторый терм с известной функцией принадлежности 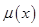, тем самым находиться количественное значение 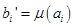. Это значение и является результатом фаззификации подусловия 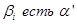. Наибольшей популярностью пользуются треугольные, а также трапецеидальные функции, рассмотренные в п.2.5.

Пример 4.12. Процесс фаззификации следующих нечетких высказываний: «водитель - молодой», «водитель - старый», «водитель - средний», для входной лингвистической переменной 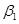- возраст водителя. Им соответствуют нечеткие высказывания вида 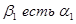, 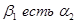и .

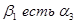Предположим, что возраст водителя равен 55 т.е. 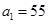. Тогда фаззификация первого нечеткого высказывания дает в результате 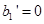, которое означает его степень истинности и получается в результате подстановки значения 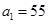в качестве значения функции принадлежности терма 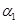- «возраст водителя - молодой». Фаззификация второго нечеткого высказывания дает число 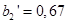. Аналогично фаззификация третьего высказывания дает .

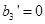Рис.4.6. Лингвистическая переменная «возраст водителя»

Агрегирование

Агрегирование представляет собой процедуру определения степени истинности условий по каждому из правил системы нечеткого вывода.

Формально процедура агрегирования выполняется следующим образом. До начала этого этапа предполагаются известными значения истинности всех подусловий системы нечеткого вывода, т.е. множество значений 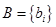. Далее рассматривается каждое из условий правил системы нечеткого вывода. Если условие правила представляет собой нечеткое высказывание вида (4.31), (4.32) и (4.33), то степень его истинности равна .

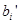Если же условие состоит из нескольких подусловий (высказываний) объединенных связками «И» и «» ИЛИ, то определяется степень истинности сложного высказывания на основе известных значений истинности подусловий по правилам преобразования (4.34) и (4.36). Тем самым находятся количественные значения истинности всех условий правил системы нечеткого вывода.

Этап агрегирования считается законченным, когда будут найдены все значения 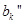для каждого из правил 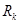, входящих в рассматриваемую базу правил системы нечеткого вывода. Это множество значений обозначим через .

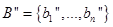Пример 4.13. Рассмотрим пример процесса агрегирования нечеткого высказывания: «возраст водителя - средний» И «возможность ДТП высокая» для входной лингвистической переменной 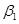- возраст водителя и 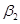- возможность совершения ДТП. Предположим, что возраст водителя 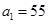, а возможность ДТП .

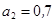Тогда агрегирование нечеткого высказывания с использованием нечеткой конъюнкции (4.34) дает .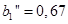

Рис.4.7. Агрегирование высказываний системы логического вывода

Активизация

Активизация в системах нечеткого вывода представляет собой процедуру или процесс нахождения степени истинности каждого их подзаключений правил нечетких продукций. Активизация определяется композицией нечетких высказываний, для определения результата нечеткой композиции используются формулы (4.35), (4.37), (4.38), (4.41). Кроме рассмотренных правил преобразований существуют и другие способы для определения функции принадлежности результата:

Max-min композиция или максиминная нечетка свертка:	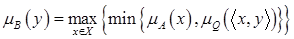;	(4.46)
Max-prod композиция:	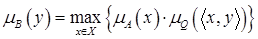;	(4.47)
Min-max композиция:	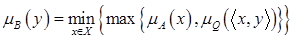;	(4.48)
Min-min композиция:	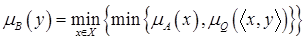;	(4.49)
Max-average композиция:	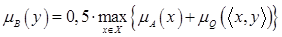.	(4.50)

В системах нечеткого вывода наиболее часто применяются методы Max-min композиции и Max-prod композиции. Метод максиминной нечеткой свертки был предложен Заде в одной из его первых работ.

Степень истинности каждого из подзаключений равна алгебраическому произведению соответствующего значении степени истинности высказывания на весовой коэффициент 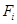. Таким образом, находятся все значения 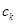степеней истинности подзаключений для каждого из правил 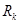, входящих в рассматриваемую базу правил системы нечеткого вывода. Это множество значений обозначим 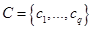, где 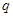- общее число подзаключений в базе правил.

После нахождения множества 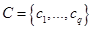определяются функции принадлежности каждого из подзаключений для рассматриваемых выходных лингвистических переменных, в общем случае (4.42). Для этой цели можно использовать и другие методы, являющиеся модификацией того или иного метода нечеткой композиции:

Min-активизация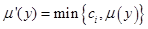

Prod-активизация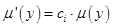

Average-активизация ,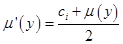

где 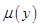- функция принадлежности терма, который является значением некоторой выходной переменной 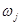, заданной на области определения .

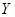Пример 4.14. Рассмотрим пример выполнения этапа активизации заключения в следующем правиле нечеткой продукции:

ЕСЛИ возраст водителя - средний ТО возможность ДТП высокая

Рис.4.8. Активизация заключений системы логического вывода

Входной лингвистической переменной в этом правиле является 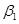- возраст водителя, а выходной 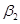- возможность совершения ДТП. Пусть возраст .

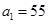Поскольку агрегирование условия дает в результате 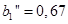, а весовой коэффициент равен 1, то значение 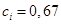. На правом рисунке заштрихованная область – график функции принадлежности лингвистической переменной высокая возможность совершения ДТП, полученный методом min-активации.

Аккумуляция

Аккумуляция или аккумулирование в системах нечеткого вывода представляет собой процедуру или процесс нахождения функции принадлежности для каждой из выходных лингвистических переменных множества .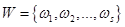

Цель аккумуляции заключается в том, чтобы объединить или аккумулировать все степени истинности заключений (подзаключений) для получения функции принадлежности каждой из выходных переменных. Необходимость выполнения этого этапа заключается в том, подзаключения, относящиеся к одной и той же выходной лингвистической переменной, принадлежат различным правилам системы нечеткого вывода.

Формально процедура аккумуляции выполняется следующим образом. До начала этапа аккумуляции полагаются известными значения истинности всех подзаключений для каждого из правил 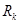, входящих в рассматриваемую базу правил системы нечеткого вывода, в форме совокупности нечетких множеств 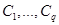, где 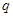- общее количество подзаключений в базе правил. Далее последовательно рассматривается каждая из выходных лингвистических переменных 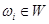и относящиеся к ней нечеткие множества 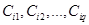. Результат аккумуляции для выходной лингвистической переменой 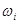определяется как объединение нечетких множеств 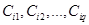. Можно использовать как max-объединение так и альтернативные операции объединения.

Пример 4.15. Рассмотрим пример процесса аккумуляции заключений для трех нечетких множеств 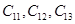, полученных в результате процедуры активизации для выходной лингвистической переменной «возраст водителя» в системе нечеткого вывода, рассмотренной в примере 4.14. Предположим, что функции принадлежности этих нечетких множеств имеют следующий вид.

Рис.4.9. Функции принадлежностей терм множеств

Тогда в результате аккумуляции этих функции принадлежности методом max-объединения получим функцию принадлежности выходной лингвистической переменной «возраст водителя» представленную на рис.4.10.

Рис.4.10. Функция принадлежности лингвистической переменной

Дефаззификация

Дефаззификация в системах нечеткого вывода представляет собой процедуру или процесс нахождения обычного (не нечеткого) значения для каждой из выходных лингвистических переменных множества .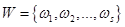

Цель дефаззификации заключается в том, чтобы, используя результаты аккумуляции всех выходных лингвистических переменных, получить обычное (не нечеткое) значение каждой из выходных переменных. Дефаззификацию также называют приведением к четкости.

Формально процедура дефаззификации выполняется следующим образом. До начала этапа дефаззификации предполагается, что известны функции принадлежности всех выходных лингвистических переменных в форме нечетких множеств 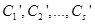, где 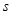- общее количество выходных лингвистических переменных в базе правил нечеткого вывода. Далее последовательно рассматривается каждая из выходных лингвистических переменных 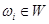и относящееся к ней нечеткое множество 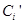. Результат дефаззификации для выходной лингвистической переменной 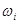определятся в виде количественного значения 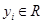, для получения которого существует ряд методов, представленных в п.2.5.

Пример 4.16. Следующая нечеткая база знаний описывает зависимость между возрастом водителя (x) и возможностью дорожно-транспортного происшествия (y):

R₁: если x_l = Молодой, то у =Высокая;

{R_i}³_i=1 = R₂: если x_l =Средний, то у = Низкая;

R₃: если x_l = Очень старый, то у = Высокая.

Пусть функции принадлежностей термов имеют вид, показанный на рис.4.6 и рис.4.7. Тогда нечеткие отношения, соответствующие правилам базы знаний, будут такими, как на рис.4.6.

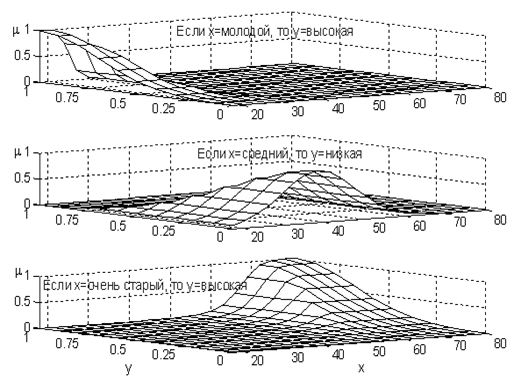
Рис.4.11. Нечеткие отношения, соответствующие правилам базы знаний

Одним из наиболее широких применений рассмотренных правил, как, впрочем, и всего аппарата нечеткой логики, является построение нечетких алгоритмов, позволяющих реализовать процесс принятия решений в условиях лингвистической неопределенности. Описание таких алгоритмов можно встретить в литературе по экспертным системам.

Нечеткий алгоритм есть упорядоченное множество нечетких инструкций, которые при их реализации дают приближенное решение проблемы.

Нечеткие алгоритмы обычно классифицируют по областям их применения:

1. Алгоритмы определения и идентификации;

2. Алгоритмы порождения;

3. Алгоритмы описания и моделирования систем;

4. Алгоритмы принятия решений и т.д.

Алгоритмы определения и идентификации.Одна из основных областей применения нечетких алгоритмов - определение сложных, плохо определенных понятий в терминах более простых или менее нечетких понятий. Например, определение меры сложности, меры похожести, диагностика болезней.

Поскольку нечеткое понятие можно рассматривать как символ нечеткого множества, алгоритм определения представляет собой конечное множество нечетких инструкций, которые определяют нечеткое множество в терминах других нечетких множеств или дают процедуру для вычисления степени принадлежности каждого элемента области рассуждений определяемому множеству.

В последнем случае алгоритм определения играет роль алгоритма идентификации, т.е. алгоритма, который устанавливает, принадлежит или нет элемент множеству, или более обще, - устанавливает его степень принадлежности.

Например, рассмотрим нечеткое понятие овал, которое приближенно эквивалентно выражению:

овал = замкнутый 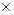не самопересекающийся 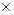выпуклый 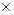более или менее ортогональные оси симметрии 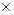большая ось несколько длиннее малой оси.

Данное выражение определяет нечеткое множество овал как пересечение обычных и нечетких множеств, символы которых стоят в правой части. Однако существенное отличие состоит в том, что алгоритм определения не только определяет правую часть, но также устанавливает порядок, в котором следует совершать эти действия.

Алгоритмы порождения служат не для определения, а порождения нечетких множеств. Возможные приложения этих алгоритмов: получение различного рода образцов, предложений в некотором языке, компьютерная графика, сочинение музыки.

Алгоритмы описания и моделирования систем служат для описания отношений между нечеткими переменными и используются для приближенного описания поведения системы. Рассмотрим пример нечеткого алгоритма отношения F(x,y).

1. Если х - мало их слабо увеличить, то у слабо увеличится.

2. Если х - мало и х значительно увеличить, то у увеличится значительно.

3. Если х - велико и х слабо увеличить, то у увеличится средне.

4. Если х - велико и х значительно увеличить, то у увеличится очень значительно.

Описание нечетких функций с помощью нечетких алгоритмов.

Такие алгоритмы позволяют приближенно описывать самые разнообразные сложные явления. Важно то, что, будучи нечеткими, по своей природе, такие описания могут быть полностью адекватны целям поставленной задачи. Нечеткие алгоритмы такого рода могут дать эффективные способы приближенного описания целевых функций, стратегий, ограничений и функционирования системы.

Алгоритмы принятия решений.Это нечеткие алгоритмы, которые служат для получения приближенного описания стратегии или решающего правила. Алгоритмы такого рода используются в системах поддержки управления.

Простой пример подобного алгоритма:

ЕСЛИ у велико ТО немного уменьшить х;

ЕСЛИ у не очень велико ТО очень не намного увеличить х;

ЕСЛИ у мало ТО стоп.

Продукционные или нечеткие системы были разработаны в рамках исследований по методам искусственного интеллекта и нашли широкое применение для представления знаний и вывода заключений в экспертных системах, основанных на правилах. Иными словами, они позволяют адекватно представить практические знания экспертов в той или иной предметной области.

Контрольные вопросы

1. В чем заключается принципиальное отличие двухзначной и многозначной логики? В каких отношениях они находятся?

2. Что такое «нечеткая» логическая формула? Приведите примеры.

3. Как определяется равносильность нечетких формул? Каков практический смысл такого определения?

4. Что такое «нечеткий предикат»? Приведите примеры.

5. Почему нечеткозначную логику называют лингвистической?

6. Какие виды высказываний используют в нечеткозначной логике? Опишите с помощью этих высказываний некоторые обычные, вербальные суждения.

7. Для чего применяются правила преобразования композиционных высказываний? Покажите практический смысл этих преобразований.

8. Как использовать лингвистическую степень истинности при оценке истинности одних нечетких высказываний относительно других?

9. Что такое база правил, и каковы основные требования, предъявляемые к ней?

10. Каковы основные этапы построения системы нечеткого вывода?

11. Каково основное предназначение нечетких алгоритмов?

Заключение

Мир вступил в эпоху информатизации, в эпоху, когда информационный ресурс становится важнейшим в жизнеобеспечении общества. Потребность в ценной, полезной информации, в интенсификации информационных процессов, процессов принятия решений явилась объективной причиной создания и бурного развития электронных вычислительных и коммуникативных средств. Широкое и эффективное внедрение этих средств в свою очередь породило стремление решать новые практические задачи в рамках более сложных моделей ускорило потребность в получении и компьютерной обработке все более сложной, нечеткой информации. Однако на этом пути возникла непреодолимая стена в виде закономерности – возрастание сложности приводит к возрастанию неопределенности, неоднозначности. Это и послужило признанием такого факта, что задачи принятия сложных решений можно формулировать только на естественном, а точнее говоря, на профессиональном языке, отражающем в полной мере специфику этих задач. Введение понятий нечеткого множества, нечеткой и лингвистической переменных сделало возможным построение достаточно строгих моделей принятия сложных решений. Другой проблемой, стоящей на пути указанной проблемы, стала эмерджентность, т.е. неожиданность, внезапность появления свойств системы, сумматативная оценка которых на основании параметров отдельных составляющих системы принципиально невозможна. Такая оценка возможна только в результате логических рассуждений, гибкость которых не укладывается в рамки жесткой двухзначной логики. Реализация моделей таких рассуждений стала реальной благодаря появлению нечеткой логики. В совокупности аппарат теории нечетких множеств и нечеткой логики позволил существенно развить компьютерную семантику [13], сделать прорыв в интеллектуализации компьютерных информационных систем. Именно эти направления являются важнейшими в современной информатике, именно с ними связывают в первую очередь надежды на успех информатизации.

Исходя из вышесказанного рассматриваемая математическая дисциплина начинает занимать обязательные позиции в системе высшего образования. Знание и умение владеть аппаратом теории нечетких множеств и нечеткой логики становится обязательным не только для специалистов, занимающихся информационным обеспечением, информационными системами, но и в других направлениях профессиональной деятельности. Об этом свидетельствуют результаты практического применения достижений этой молодой теории в различных сферах [3, 8, 14, 15, 16]. В силу того, что дух теории нечетких множеств выражается прежде всего в систематическом, нежели количественном методе обработки нечеткой информации, представляется наиболее перспективным ее применение в лингвистике, документалистике, психологии, социологии, политологии и других гуманитарных науках, где чаще всего приходится сталкиваться с субъективным фактором. Вполне очевидной становится значительная роль этой теории в экономических исследованиях, в экономико-математическом моделировании, в управлении социальными и экономическими системами.